Project Periodic Geometry within a new area of Geometric Data Science based on papers in
SIAP 2026
Pattern Recognition 2026
SIMODS 2025
ACA 2025
IUCrJ 2024
SISC 2023
NeurIPS 2022
PRE 2022
MATCH 2022
DGMM 2021
- Periodic Geometry develops continuous parametrizations for moduli spaces of periodic objects under rigid motion.
- The subarea of Lattice Geometry studies moduli spaces of simpler periodic lattices in low dimensions 2 and 3.
- The subarea of Density Functions studies generically complete isometry invariants extending the crystal density.
- The adjacent area of Cloud Isometry Spaces studies geometry of moduli spaces of finite clouds of unordered points.
- The related area of Structure-Property Relations aims to explain all properties of a structure in terms of its invariants.
- The applied area of Computational Materials Science explores practical applications of geometric invariants and metrics.
- The wider area of Geometric Data Science studies moduli spaces of any data objects under practical equivalences.
- The latest developments are discussed in the MIF++ seminar and at the annual conference MACSMIN since 2020.
Pointwise Distance Distribution (PDD)
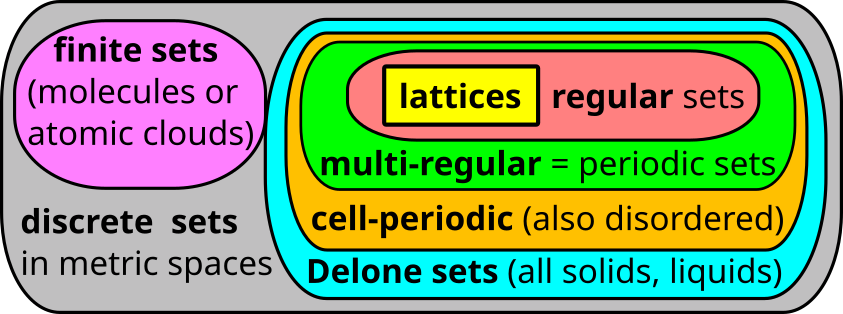 |
|
- Abstract.
Many real objects are modeled as discrete sets of points, such as corners or other salient features. For our main applications in chemistry, points represent atomic centers in a molecule or a solid material. We study the problem of classifying discrete (finite and periodic) sets of unordered points under isometry, which is any transformation preserving distances in a metric space.
Experimental noise motivates the new practical requirement to make such invariants Lipschitz continuous so that perturbing every point in its epsilon-neighborhood changes the invariant up to a constant multiple of epsilon in a suitable distance satisfying all metric axioms. Since the given points are unordered, the key challenge is to compute all invariants and metrics in a near-linear time of the input size.
We define the Pointwise Distance Distribution (PDD) for any discrete set and prove, in addition to the properties above, the completeness of PDD for all periodic sets in general position. The PDD can compare nearly 2 million crystals from the world's five largest databases within 2 hours on a modest desktop computer. The impact is upholding data integrity in crystallography because the PDD will not allow anyone to claim a `new' material as a noisy disguise of a known crystal. @article{widdowson2026pointwise, author = {Daniel Widdowson and Vitaliy Kurlin}, title = {Pointwise Distance Distributions for detecting near-duplicates in large materials databases}, journal = {SIAM Journal on Applied Mathematics}, doi={10.1137/25M1736657}, year = {2026} }
Back to Top of this page | Back to Research & papers | Back to Home page
Recognition of near-duplicate periodic patterns
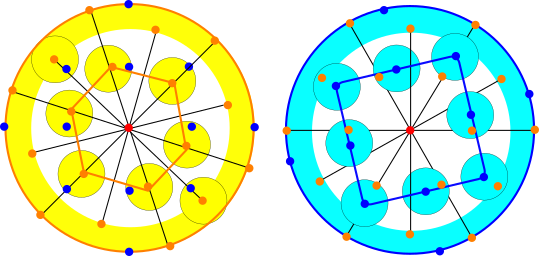 |
|
- Abstract. This paper rigorously solves the challenging problem of recognizing periodic patterns under rigid motion in Euclidean geometry. The 3-dimensional case is practically important for justifying the novelty of solid crystalline materials (periodic crystals) and for patenting medical drugs in a solid tablet form. Past descriptors based on finite subsets fail when a unit cell of a periodic pattern discontinuously changes under almost any perturbation of atoms, which is inevitable due to noise and atomic vibrations. The major problem is not only to find complete invariants (descriptors with no false negatives and no false positives for all periodic patterns) but to design efficient algorithms for distance metrics on these invariants that should continuously behave under noise. The proposed continuous metrics solve this problem in any Euclidean dimension and are algorithmically approximated with small error factors in times that are explicitly bounded in the size and complexity of a given pattern. The proved Lipschitz continuity allows us to confirm all near-duplicates filtered by simpler invariants in major databases of experimental and simulated crystals. This practical detection of noisy duplicates will stop the artificial generation of `new' materials from slight perturbations of known crystals. Several such duplicates are under investigation by five journals for data integrity.
@article{anosova2026recognition, author = {Olga Anosova and Daniel Widdowson and Vitaliy Kurlin}, title = {Recognition of near-duplicate periodic patterns by continuous metrics with approximation guarantees}, journal = {Pattern Recognition}, volume={171}, number={112108}, year = {2026} }
Back to Top of this page | Back to Research & papers | Back to Home page
Complete invariants of 1-periodic sequences
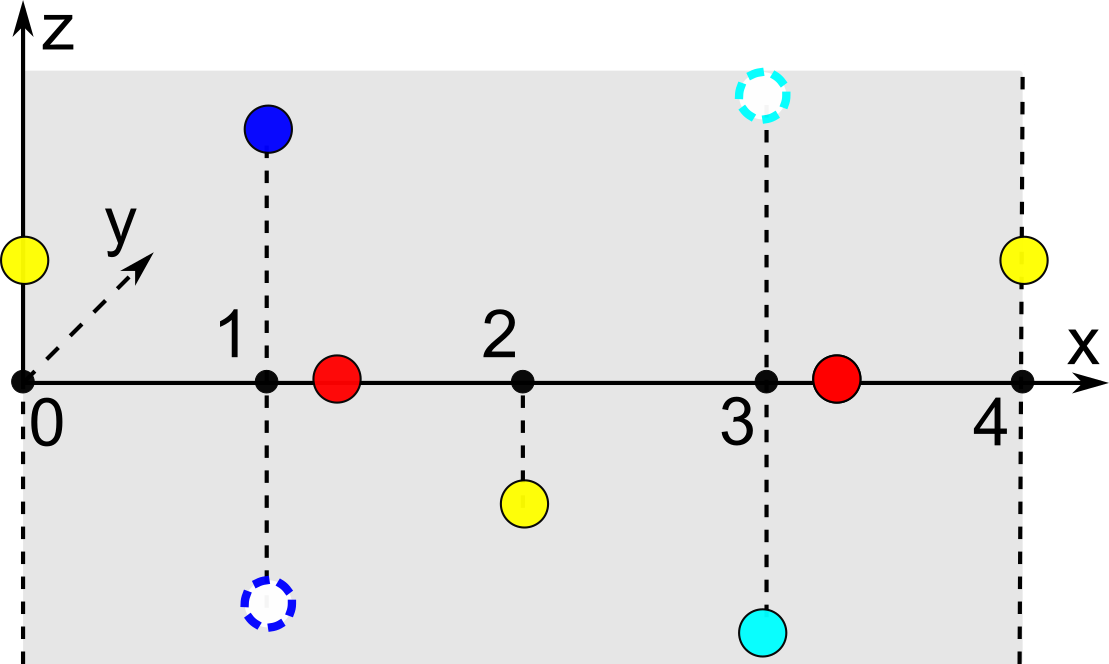 |
|
- Abstract. Inevitable noise in real measurements motivates the challenging problem of continuously quantifying the similarity between rigid objects such as periodic time series and 1-dimensional materials considered under isometry maintaining inter-point distances. The past work developed many Hausdorff-like distances, which have slow or approximate algorithms due to minimizations over infinitely many isometries. For all finite and 1-periodic sequences under isometry and rigid motion in any high-dimensional Euclidean space, we introduce complete invariants and Lipschitz continuous metrics whose time complexities are polynomial in both input size and ambient dimension. The key novelty in the periodic case is the Lipschitz continuity under perturbations that discontinuously change a minimum period. The proven continuity is practically important for maintaining scientific integrity by real-time detection of near-duplicate structures in experimental and simulated materials datasets.
@article{kurlin2025complete, author = {Vitaliy Kurlin}, title = {Complete and continuous invariants of 1-periodic sequences in polynomial time}, journal = {SIAM Journal on Mathematics of Data Science}, volume = {7}, issue = {4}, pages = {1643-1663}, year = {2025} }
Back to Top of this page | Back to Research & papers | Back to Home page
The bridge length of a periodic point set
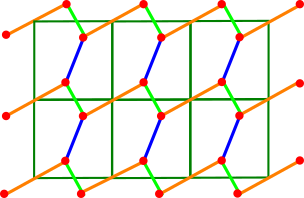 |
|
- Abstract. The fundamental model of any periodic crystal is a periodic set of points at all atomic centres. Since crystal structures are determined in a rigid form, their strongest equivalence is rigid motion (composition of translations and rotations) or isometry (also including reflections). The recent classification of periodic point sets under rigid motion used a complete invariant isoset whose size essentially depends on the bridge length, defined as the minimum `jump' that suffices to connect any points in the given set. We propose a practical algorithm to compute the bridge length of any periodic point set given by a motif of points in a periodically translated unit cell. The algorithm has been tested on a large crystal dataset and is required for an efficient continuous classification of all periodic crystals. The exact computation of the bridge length is a key step to realising the inverse design of materials from new invariant values.
@article{mcmanus2025computing, author = {Jonathan McManus and Vitaliy Kurlin}, title = {Computing the bridge length: the key ingredient in a continuous isometry classification of periodic point sets}, journal = {Acta Cryst A}, volume = {81}, issue={6}, pages={427-437}, year = {2025} }
Back to Top of this page | Back to Research & papers | Back to Home page
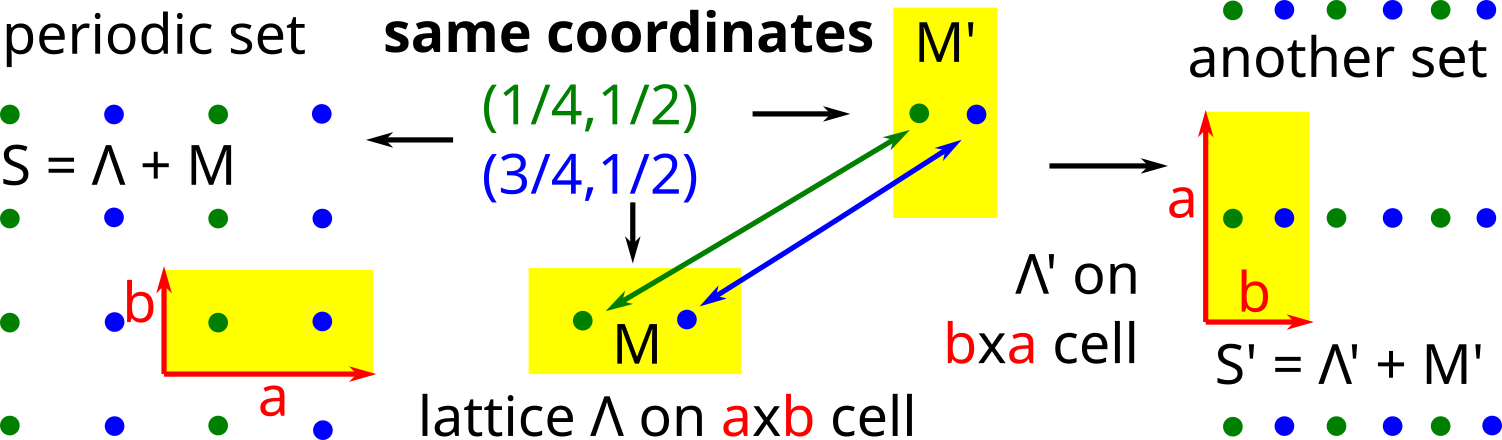
New definition of a crystal (periodic) structure
 |
|
- Abstract. This paper was motivated by the articles ``Same or different - that is the question'' in CrystEngComm (July 2020) and ``Change to the definition of a crystal'' in the IUCr newsletter (June 2021). Experimental approaches to crystal comparisons require rigorously defined classifications in crystallography and beyond. Since crystal structures are determined in a rigid form, their strongest equivalence in practice is rigid motion, which is a composition of translations and rotations in 3-dimensional space. Conventional representations based on reduced cells and standardizations theoretically distinguish all periodic crystals. However, all cell-based representations are inherently discontinuous under almost any atomic displacement that can arbitrarily scale up a reduced cell. Hence comparing millions of known structures in materials databases needs continuous distance metrics.
@article{anosova2024importance, author = {Olga Anosova and Vitaliy Kurlin and Marjorie Senechal}, title = {The importance of definitions in crystallography}, journal = {IUCrJ}, volume = {11}, issue = {4}, pages = {453-463}, doi = {10.1107/S2052252524004056}, year = {2024} }
Back to Top of this page | Back to Research & papers | Back to Home page
Densest Crystallographic Group Packings
 |
|
- Abstract. Molecular crystal structure prediction (CSP) seeks the most stable periodic structure given the chemical composition of molecule and pressure-temperature conditions. Modern CSP solvers use global optimization methods to search for structures with minimal free energy within a complex energy landscape induced by intermolecular potentials. A major caveat of these methods is that initial configurations are random, making the search susceptible to convergence at local minima. Providing initial configurations that are densely packed with respect to the geometric representation of a molecule can significantly accelerate CSP. Motivated by these observations, we define a class of periodic packings restricted to crystallographic symmetry groups (CSG) and design a search method for the densest CSG packings in an information-geometric framework. Since CSG induces a toroidal topology on the configuration space, a non-Euclidean trust region method is performed on a statistical manifold consisting of probability distributions defined on an n-dimensional flat unit torus by extending the multivariate von Mises distribution. Introducing an adaptive quantile reformulation of the fitness function into the optimization schedule provides the algorithm with a geometric characterization through local dual geodesic flows. Moreover, we examine the geometry of the adaptive selection-quantile defined trust region and show that the algorithm performs a maximization of stochastic dependence among elements of the extended multivariate von Mises distributed random vector. We experimentally evaluate the behavior and performance of the algorithm on various densest packings of convex polygons in 2-dimensional CSGs for which optimal solutions are known, and we demonstrate its application in the pentacene thin-film CSP.
@article{torda2023entropic, author = {Milo Torda and John Goulermas and Roland Púček and Vitaliy Kurlin}, title = {Entropic Trust Region for Densest Crystallographic Symmetry Group Packings}, journal = {SIAM Journal on Scientific Computing}, doi = {10.1137/22M147983X}, volume = {45}, number = {4}, pages = {B493-B522}, year = {2023} }
Back to Top of this page | Back to Research & papers | Back to Home page
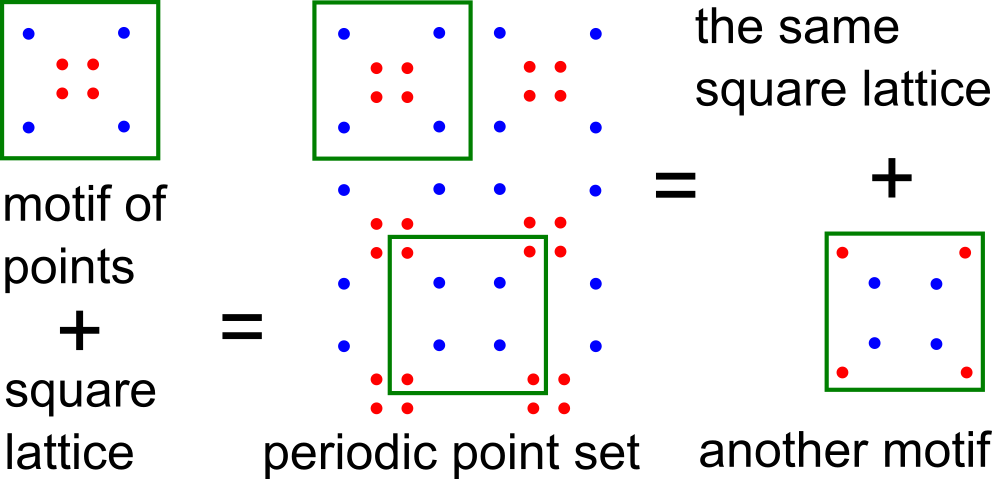
Resolving the data ambiguity for periodic crystals
|
|
- Abstract. The fundamental model of all solid crystalline materials (periodic crystals) is a periodic set of atomic centers considered under rigid motion in Euclidean space. The major obstacle to materials discovery was highly ambiguous representations that didn't allow fast and reliable comparisons, and led to numerous (near-) duplicates in all experimental databases. This paper introduces the new invariants that are crystal descriptors without false negatives and are called Pointwise Distance Distributions (PDD). The PDD invariants are numerical matrices with a near-linear time complexity and an exactly computable metric. The strongest theoretical result is generic completeness (absence of false positives) for all finite and periodic sets of points in any dimension. The strength of PDD is demonstrated by 200B+ pairwise comparisons of all 660K+ periodic structures from the world's largest Cambridge Structural Database of 1.17M+ known crystals over two days on a modest desktop.
@article{widdowson2022resolving, author = {Daniel Widdowson and Vitaliy Kurlin}, title = {Resolving the data ambiguity for periodic crystals}, journal = {Advances in Neural Information Processing Systems (Proceedings of NeurIPS 2022)}, volume = {35}, pages = {24625--24638}, year = {2022} }
Back to Top of this page | Back to Research & papers | Back to Home page
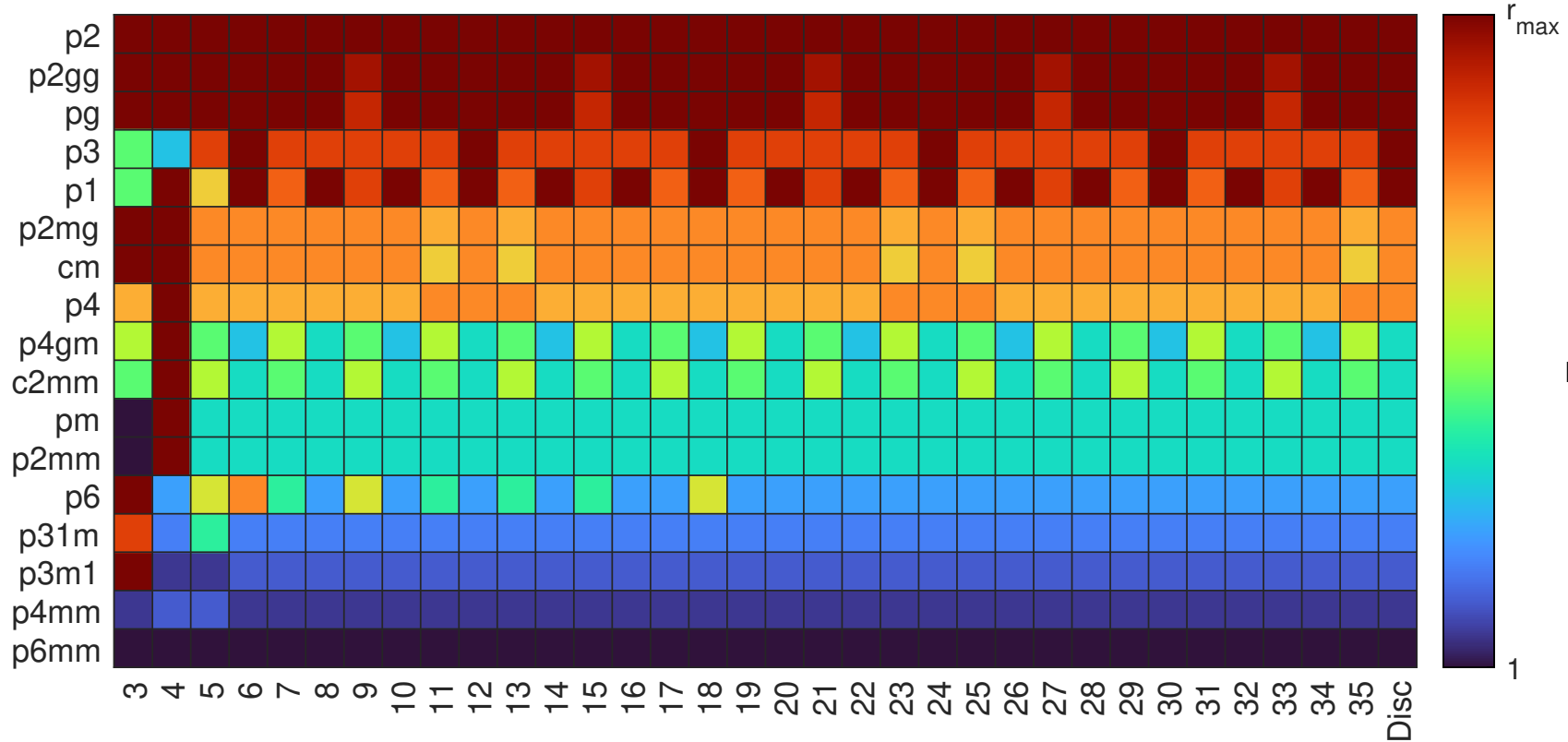
Densest packings of regular polygons
 |
|
- Abstract. Packings of regular convex polygons (n-gons) that are sufficiently dense have been studied extensively in the context of modeling physical and biological systems as well as discrete and computational geometry. Former results were mainly regarding densest lattice or double-lattice configurations. Here we consider all 2-dimensional crystallographic symmetry groups (plane groups) by restricting the configuration space of the general packing problem of congruent copies of a compact subset of the 2-dimensional Euclidean space to particular isomorphism classes of the discrete group of isometries. We formulate the plane group packing problem as a nonlinear constrained optimization problem. By means of the Entropic Trust Region Packing Algorithm that approximately solves this problem, we examine some known and unknown densest packings of various n-gons in all 17 plane groups and state conjectures about common symmetries of the densest plane group packings for every n-gon.
@article{torda2022densest, author = {Miloslav Torda and John Y Goulermas and Vitaliy A Kurlin and Graeme M Day}, title = {Densest plane group packings of regular polygons}, journal = {Physical Review E}, volume = {106}, issue = {5}, pages = {054603}, year = {2022} }
Back to Top of this page | Back to Research & papers | Back to Home page
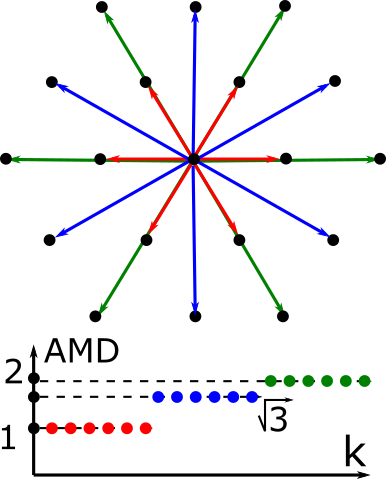
Average Minimum Distances of periodic point sets

|
|
- Abstract. The fundamental model of any solid crystalline material (crystal) at the atomic scale is a periodic point set. The strongest natural equivalence of crystals is rigid motion or isometry that preserves all inter-atomic distances. Past comparisons of periodic structures often used manual thresholds, symmetry groups and reduced cells, which are discontinuous under perturbations or thermal vibrations of atoms. This work defines the infinite sequence of continuous isometry invariants (Average Minimum Distances) to progressively capture distances between neighbours. The asymptotic behaviour of the new invariants is theoretically proved in all dimensions for a wide class of sets including non-periodic. The proposed near linear time algorithm identified all different crystals in the world's largest Cambridge Structural Database over a few hours on a modest desktop. The computational strength provides rigorous foundations to continuously parametrise the space of all real periodic crystals as a high-dimensional extension of Mendeleev's periodic table of elements.
@article{widdowson2022average, author = {Daniel Widdowson and Marco Mosca and Angeles Pulido and Andrew Cooper and Vitaliy Kurlin}, title = {Average Minimum Distances of periodic point sets - foundational invariants for mapping all periodic crystals}, journal = {MATCH Communications in Mathematical and in Computer Chemistry}, doi = {10.46793/match.87-3.529W}. volume = {87}, issue = {3}, pages = {529-559}, year = {2022} }
Back to Top of this page | Back to Research & papers | Back to Home page
Crystal isosets are complete isometry invariants
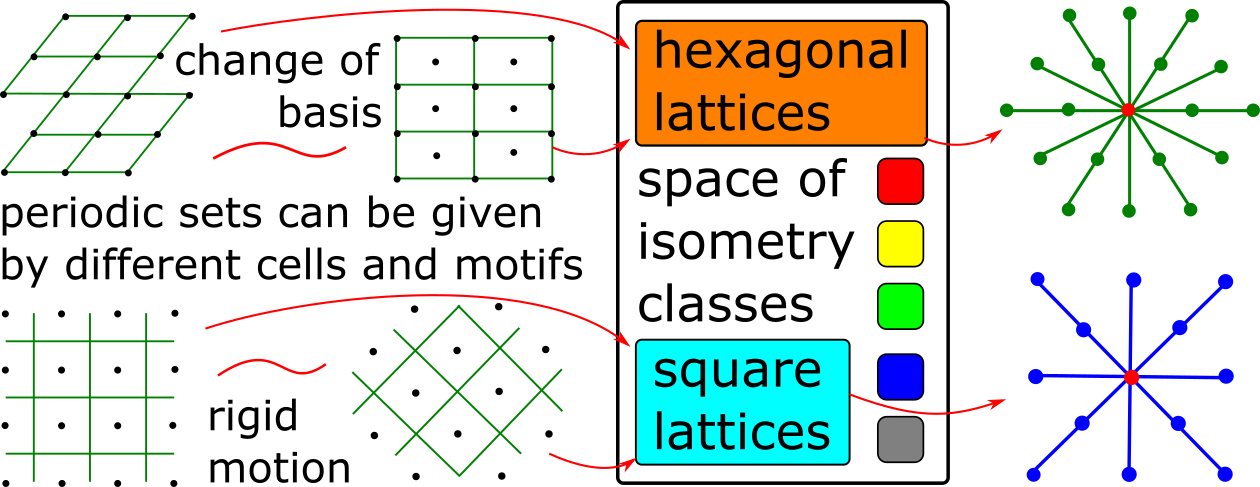 |
|
- Abstract. We develop discrete geometry methods to resolve the data ambiguity challenge for periodic point sets to accelerate materials discovery. In any high-dimensional Euclidean space, a periodic point set is obtained from a finite set (motif) of points in a parallelepiped (unit cell) by periodic translations of the motif along basis vectors of the cell. An important equivalence of periodic sets is a rigid motion or an isometry that preserves interpoint distances. This equivalence is motivated by solid crystals whose periodic structures are determined in a rigid form. Crystals are still compared by descriptors that are either not isometry invariants or depend on manually chosen tolerances or cut-off parameters. All discrete invariants including symmetry groups can easily break down under atomic vibrations, which are always present in real crystals. We introduce a complete isometry invariant for all periodic sets of points, which can additionally carry labels such as chemical elements. The main classification theorem says that any two periodic sets are isometric if and only if their proposed complete invariants (called isosets) are equal. A potential equality between isosets can be checked by an algorithm, whose computational complexity is polynomial in the number of motif points. The key advantage of isosets is continuity under perturbations, which allows us to quantify similarities between any periodic sets.
@inproceedings{anosova2021isometry, author = {Anosova, Olga and Kurlin, Vitaliy}, title = {An isometry classification of periodic point sets}, booktitle = {Lecture Notes in Computer Science (Proceedings of DGMM)}, doi = {10.1007/978-3-030-76657-3_16}, volume = {12708}, pages = {229-241}, year = {2021} }
Back to Top of this page | Back to Research & papers | Back to Home page
