Project Density Functions within a new area of Geometric Data Science based on papers in
JMIV 2023
ISVC 2022
DGMM 2022
SoCG 2021
- Density Functions are generically complete isometry invariants extending the crystal density to other periodic objects.
- The wider area of Periodic Geometry studies moduli spaces of general periodic point sets that model all periodic crystals.
- The related area of Cloud Isometry Spaces studies geometry of moduli spaces for finite clouds of unlabeled points.
- The applied area of Computational Materials Science explores practical applications of geometric invariants and metrics.
- The new research area of Geometric Data Science studies moduli spaces of any data objects up to practical equivalences.
- The latest developments are discussed in the MIF++ seminar and at the annual conference MACSMIN since 2020.
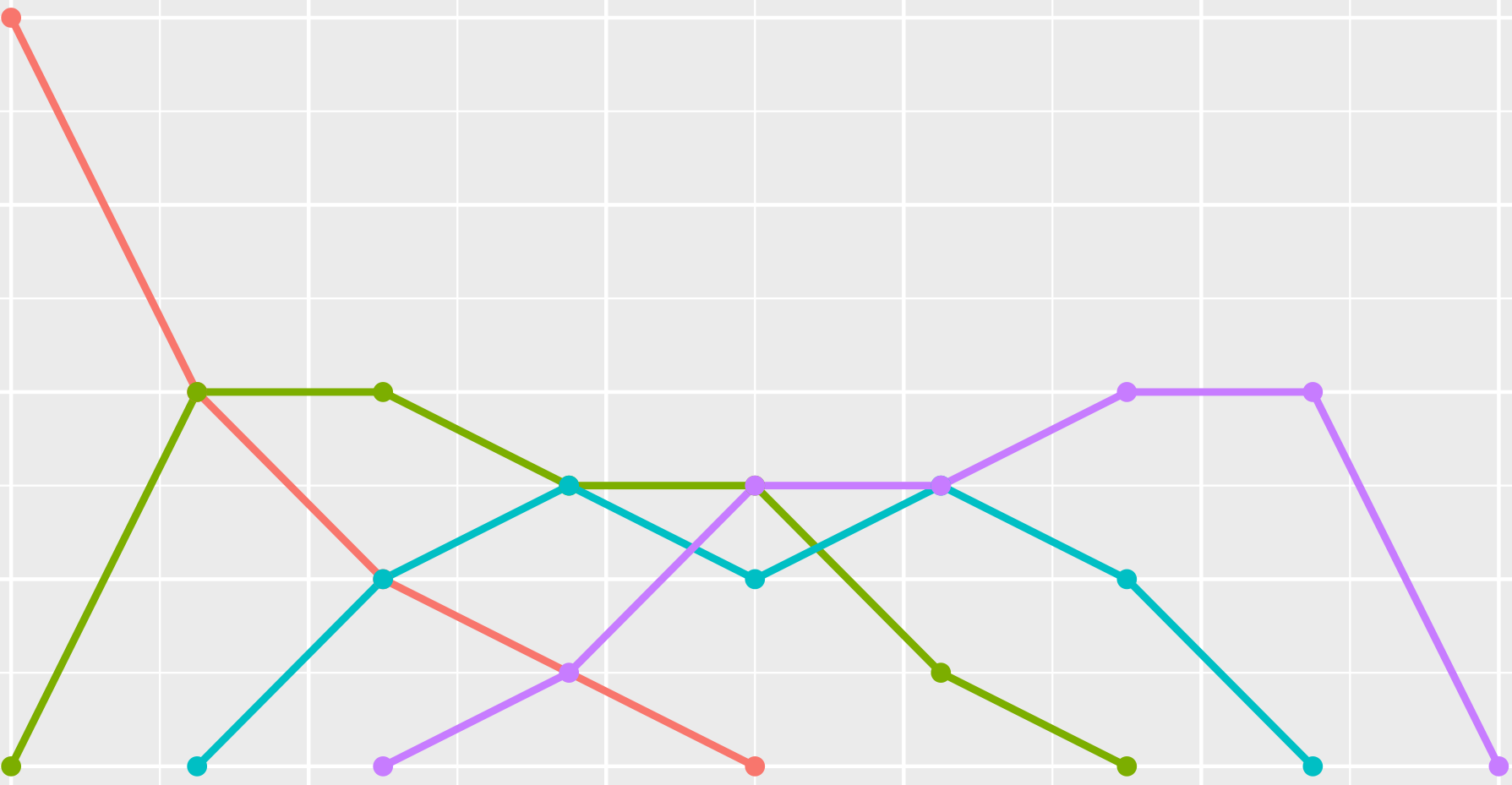
Density functions of continuous events
|
|
- DOI : 10.1007/s10851-023-01150-1
- Abstract. Periodic Geometry studies isometry invariants of periodic point sets that are also continuous under perturbations. The motivations come from periodic crystals whose structures are determined in a rigid form but any minimal cells can discontinuously change due to small noise in measurements. For any integer k>=0, the density function of a periodic set S was previously defined as the fractional volume of all k-fold intersections (within a minimal cell) of balls that have a variable radius t and centers at all points of S. This paper introduces the density functions for periodic sets of points with different initial radii motivated by atomic radii of chemical elements and by continuous events occupying disjoint intervals in time series. The contributions are explicit descriptions of the densities for periodic sequences of intervals. The new densities are strictly stronger and distinguish periodic sequences that have identical densities in the case of zero radii.
@article{anosova2023density, title={Density functions of periodic sequences of continuous events}, author={Olga Anosova and Vitaliy Kurlin}, journal={Journal of Mathematical Imaging and Vision}, volume={65}, pages={689–701}, year={2023} }
Back to Top of this page | Back to Research & papers | Back to Home page
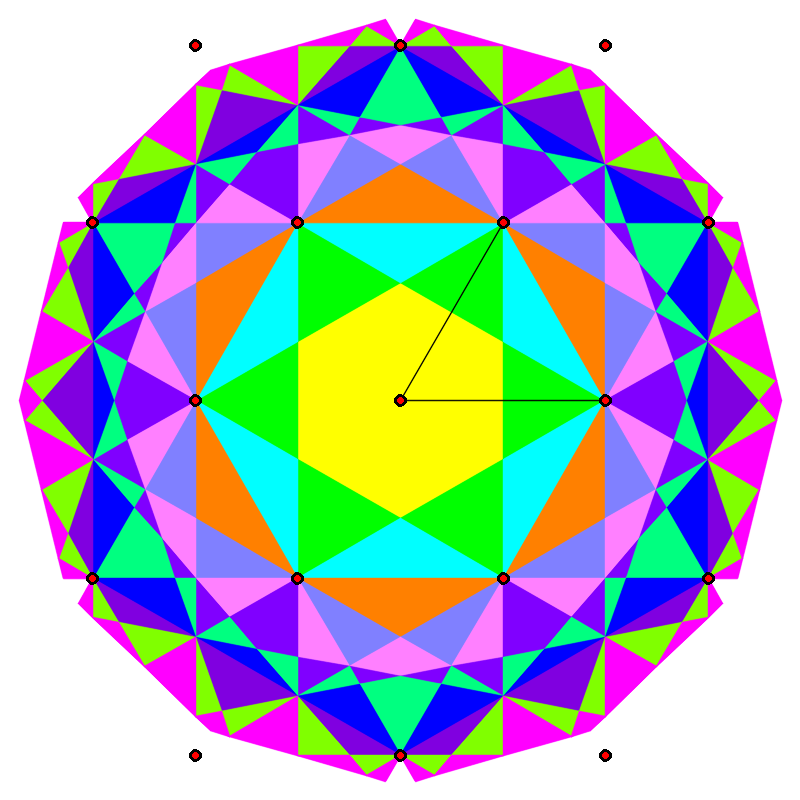
Higher degree Voronoi domains of periodic point sets
|
|
- DOI : 10.1007/978-3-031-20713-6_29
- Abstract. Degree-k Voronoi domains of a periodic point set are concentric regions around a fixed centre consisting of all points in Euclidean space that have the centre as their k-th nearest neighbour. Periodic point sets generalise the concept of a lattice by allowing multiple points to appear within a unit cell of the lattice. Thus, periodic point sets model all solid crystalline materials (periodic crystals), and degree-k Voronoi domains of periodic point sets can be used to characterise the relative positions of atoms in a crystal from a fixed centre. The paper describes the first algorithm to compute all degree-k Voronoi domains up to any degree k>0 for any two or three-dimensional periodic point set.
@inproceedings{smith2022practical, title={A practical algorithm for degree-k Voronoi domains of three-dimensional periodic point sets}, author={Phil Smith and Vitaliy Kurlin}, booktitle={Lecture Notes in Computer Science (Proceedings of ISVC)}, volume={13599}, pages={377-391}, year={2022} }
Back to Top of this page | Back to Research & papers | Back to Home page
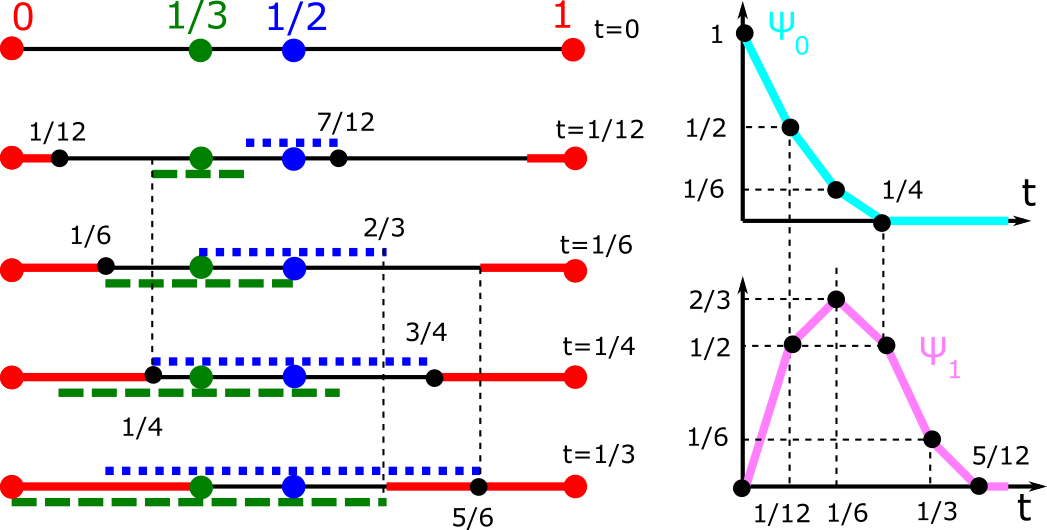
Density functions of periodic sequences
|
|
- DOI : 10.1007/978-3-031-19897-7_31
- Abstract. This paper contributes to the emergent area of Periodic Geometry, which studies continuous spaces of solid crystalline materials (crystals) by new methods of metric geometry. Since crystal structures are determined in a rigid form, their strongest practical equivalence is rigid motion or isometry preserving inter-point distances. The most fundamental model of any crystal is a periodic set of points at all atomic centers. The previous work introduced an infinite sequence of density functions that are continuous isometry invariants of periodic point sets. These density functions turned out to be highly non-trivial even in dimension 1 for periodic sequences of points in the line. This paper fully describes the density functions of any periodic sequence and their symmetry properties. The explicit description confirms coincidences of density functions that were previously computed only through finite samples.
@inproceedings{anosova2022density, title={Density functions of periodic sequences}, author={Olga Anosova and Vitaliy Kurlin}, booktitle={Lecture Notes in Computer Science (Proceedings of DGMM)}, volume={13493}, pages={395-408}, year={2022} }
Back to Top of this page | Back to Research & papers | Back to Home page
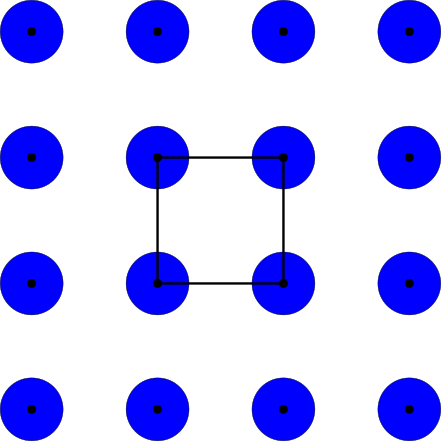
Density functions of a periodic point set

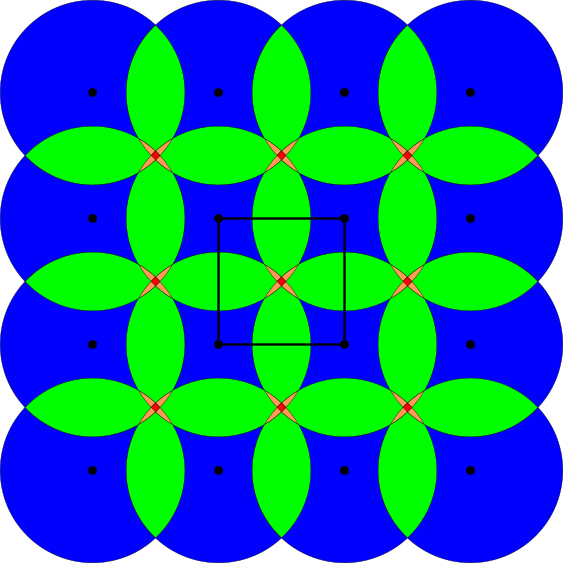
 |
|
- DOI : 10.4230/LIPIcs.SoCG.2021.32
- Abstract. Modeling a crystal as a periodic point set, we present a fingerprint consisting of density functions that facilitates the efficient search for new materials. We prove invariance under isometries, continuity, and completeness in the generic case, which are necessary features for the reliable comparison of crystals. The proof of continuity integrates methods from discrete geometry and lattice theory, while the proof of generic completeness combines techniques from geometry with analysis. The fingerprint has a fast algorithm based on Brillouin zones and related inclusion-exclusion formulae. We have implemented the algorithm and describe its application to crystal structure prediction.
@inproceedings{edelsbrunner2021density, title={The Density Fingerprint of a Periodic Point Set}, author={Herbert Edelsbrunner and Teresa Heiss and Vitaliy Kurlin and Philip Smith and Mathijs Wintraecken}, booktitle={Proceedings of Symposium on Computational Geometry}, volume={189}, pages={32:1--32:16}, year={2021} }
Back to Top of this page | Back to Research & papers | Back to Home page
