Lattice Geometry within a new area of Geometric Data Science based on papers in
FoCM 2024
Chirality 2023
ACA 2023
CRaT 2020
CCCG 2015
- Lattice Geometry develops continuous parametrizations and metrics for moduli spaces of lattices up to isometry.
- The wider area of Periodic Geometry studies moduli spaces of general periodic point sets that model all periodic crystals.
- The related area of Cloud Isometry Spaces studies geometry of moduli spaces of finite clouds of unlabeled points.
- The even wider area of Geometric Data Science studies moduli spaces of any data objects up to practical equivalences.
- The applied area of Computational Materials Science explores practical applications of geometric invariants and metrics.
- The latest developments are discussed in the MIF++ seminar and at the annual conference MACSMIN since 2020.
Mathematics of 2D lattices

|
|
- Abstract. A periodic lattice in Euclidean space is the infinite set of all integer linear combinations of basis vectors. Any lattice can be generated by infinitely many different bases. This ambiguity was only partially resolved but standard reductions remain discontinuous under perturbations modelling crystal vibrations. This paper completes a continuous classification of 2-dimensional lattices up to Euclidean isometry (or congruence), rigid motion (without reflections), and similarity (with uniform scaling). The new homogeneous invariants allow easily computable metrics on lattices considered up to the equivalences above. The metrics up to rigid motion are especially non-trivial and settle all remaining questions on (dis)continuity of lattice bases. These metrics lead to real-valued chiral distances that continuously measure lattice deviations from higher-symmetry neighbours. The geometric methods extend the work of Delone, Conway, and Sloane.
@article{kurlin2024mathematics, title={Mathematics of 2-dimensional lattices}, author={Vitaliy A Kurlin}, journal={Foundations of Computational Mathematics}, volume={24}, pages={805–863}, doi={10.1007/s10208-022-09601-8}, year={2024} }
Back to Top of this page | Back to Research & papers | Back to Home page
Continuous chiral distances for 2D lattices
|
|
- DOI : doi:10.1002/chir.23598
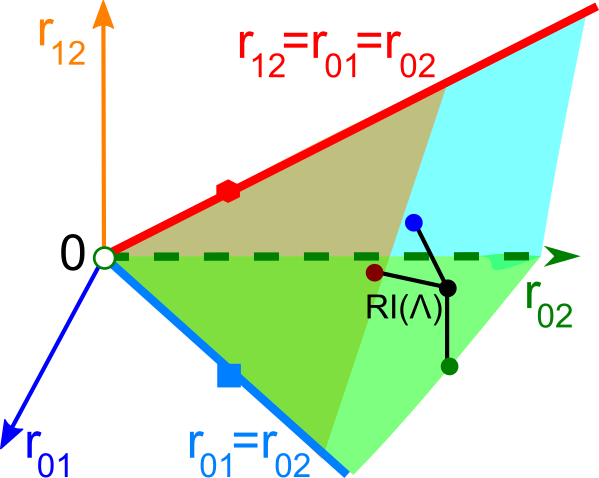
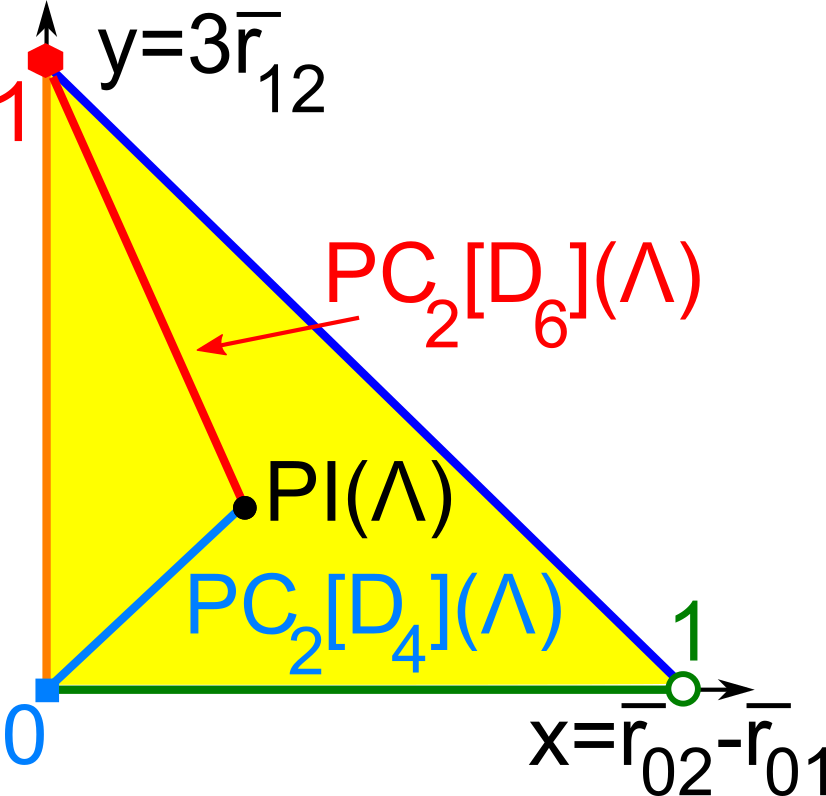
- Abstract. Chirality was traditionally considered a binary property of periodic lattices and crystals. However, the classes of 2-dimensional lattices modulo rigid motion form a continuous space, which was recently parametrized by three geographic-style coordinates. The four non-oblique Bravais classes of 2-dimensional lattices form low-dimensional singular subspaces in the full continuous space. Now the deviations of a lattice from its higher symmetry neighbours can be continuously quantified by real-valued distances satisfying metric axioms. This paper analyses these and newer G-chiral distances for millions of 2-dimensional lattices that are extracted from publicly available databases of 2-dimensional structures and real materials in the Cambridge Structural Database.
@article{bright2023continuous, title={Continuous chiral distances for 2-dimensional lattices}, author={Matthew J Bright and Andrew I Cooper and Vitaliy A Kurlin}, journal={Chirality}, volume={35}, issue={12}, pages={920-936}, year={2023} }
Back to Top of this page | Back to Research & papers | Back to Home page
Geographic-style maps for 2D lattices

|
|
- DOI : 10.1107/S2053273322010075
- Abstract. This paper develops geographic-style maps containing 2D lattices in all known periodic crystals parameterised by recent complete invariants. Motivated by rigid crystal structures, lattices are considered up to rigid motion and uniform scaling. The resulting space of 2D lattices is a square with identified edges or a punctured sphere. The new continuous maps show all Bravais classes as low-dimensional subspaces, visualise hundreds of thousands of real crystal lattices from the Cambridge Structural Database, and motivate the development of continuous and invariant-based crystallography.
@article{bright2023geographic, title={Geographic-style maps for 2-dimensional lattices}, author={Matthew J Bright and Andrew I Cooper and Vitaliy A Kurlin}, journal={Acta Crystallographica Section A}, volume ={79}, number ={1}, pages={1-13}, year={2023} }
Back to Top of this page | Back to Research & papers | Back to Home page
Voronoi-based metrics on lattices
 |
|
- DOI : 10.1002/crat.201900197
- Abstract. This paper develops a new continuous approach to a similarity between periodic lattices of ideal crystals. Quantifying a similarity between crystal structures is needed to substantially speed up the Crystal Structure Prediction, because the prediction of many target properties of crystal structures is computationally slow and is essentially repeated for many nearly identical simulated structures. The proposed distances between arbitrary periodic lattices of crystal structures are invariant under all rigid motions, satisfy the metric axioms and continuity under atomic perturbations. The above properties make these distances ideal tools for clustering and visualizing large datasets of crystal structures. All the conclusions are rigorously proved and justified by experiments on real and simulated crystal structures reported in the Nature 2017 paper Functional materials discovery using energy–structure–function maps.
@article{mosca2020voronoi, title={Voronoi-based similarity distances between arbitrary crystal lattices}, author={Mosca, Marco and Kurlin, Vitaliy}, journal={Crystal Research and Technology}, volume={55}, number={5}, pages={190-197}, year={2020} }
Back to Top of this page | Back to Research & papers | Back to Home page
Relaxed disk packing
 |
|
- Abstract. Motivated by biological questions, we study configurations of equal-sized disks in the Euclidean plane that neither pack nor cover. Measuring the quality by the probability that a random point lies in exactly one disk, we show that the regular hexagonal grid gives the maximum among lattice configurations.
@inproceedings{edelsbrunner2015relaxed, author = {Herbert Edelsbrunner and Mabel Iglesias-Ham and Vitaliy A Kurlin}, title = {Relaxed disk packing}, booktitle = {Proceedings of CCCG 2015: Canadian Conference on Computational Geometry}, year = {2015} }
Back to Top of this page | Back to Research & papers | Back to Home page
