Project Structure-Property Relations within a new area of Geometric Data Science based on
SR 2024
IMMI 2024
RCR 2024
DAMDID 2022
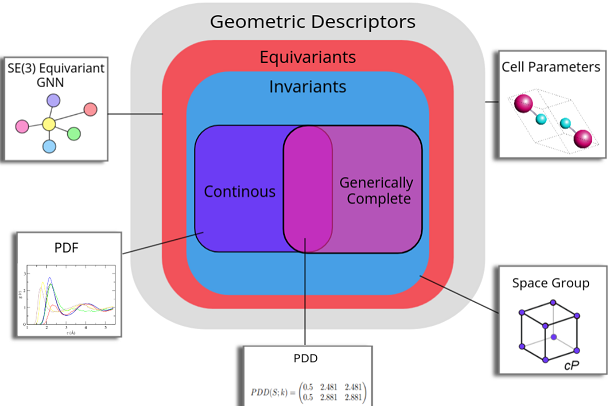
- Structure-Property Relations aim to explain all properties of a molecular or crystal structure by its invariants.
- The related area of Periodic Geometry develops continuous parametrisations for moduli spaces of periodic point sets.
- The adjacent area of Cloud Isometry Spaces studies geometry of moduli spaces of finite clouds of unlabeled points.
- The applied area of Computational Materials Science explores practical applications of geometric invariants and metrics.
- The wider area of Geometric Data Science studies moduli spaces of any data objects up to practical equivalences.
- The latest developments are discussed in the MIF++ seminar and at the annual conference MACSMIN since 2020.
Faster property prediction by isometry invariants
 |
|
- Abstract. Periodic material or crystal property prediction using machine learning has grown popular in recent years as it provides a computationally efficient replacement for classical simulation methods. A crucial first step for any of these algorithms is the representation used for a periodic crystal. While similar objects like molecules and proteins have a finite number of atoms and their representation can be built based upon a finite point cloud interpretation, periodic crystals are unbounded in size, making their representation more challenging. In the present work, we adapt the Pointwise Distance Distribution (PDD), a continuous and generically complete isometry invariant for periodic point sets, as a representation for our learning algorithm. The PDD distinguished all (more than 660 thousand) periodic crystals in the Cambridge Structural Database as purely periodic sets of points without atomic types. We develop a transformer model with a modified self-attention mechanism that combines PDD with compositional information via a spatial encoding method. This model is tested on the crystals of the Materials Project and Jarvis-DFT databases and shown to produce accuracy on par with state-of-the-art methods while being several times faster in both training and prediction time.
@article{balasingham2024accelerating, author={Jonathan Balasingham and Viktor Zamaraev and Vitaliy Kurlin}, title = {Accelerating Material Property Prediction using Generically Complete Isometry Invariants}, journal = {Scientific Reports}, volume={14}, pages={10132}, year = {2024} }
Back to Top of this page | Back to Research & papers | Back to Home page
Material property prediction by graph invariants
 |
|
- DOI : 10.1007/s40192-024-00351-9
- Abstract. The structure-property hypothesis says that the properties of all materials are determined by an underlying crystal structure. The main obstacle was the ambiguity of conventional crystal representations based on incomplete or discontinuous descriptors that allow false negatives or false positives. This ambiguity was resolved by the ultra-fast Pointwise Distance Distribution (PDD), which distinguished all periodic structures in the world’s largest collection of real materials (Cambridge Structural Database). The state-of-the-art results in property predictions were previously achieved by graph neural networks based on various graph representations of periodic crystals, including the Crystal Graph with vertices at all atoms in a crystal unit cell. This work adapts the Pointwise Distance Distribution for a simpler graph whose vertex set is not larger than the asymmetric unit of a crystal structure. The new Distribution Graph reduces mean-absolute-error by 0.6%-12% while having 44%-88% of the number of vertices when compared to the crystal graph when applied on the Materials Project and Jarvis-DFT datasets using CGCNN and ALIGNN. Methods for hyper-parameters selection for the graph are backed by the theoretical results of the Pointwise Distance Distribution and are then experimentally justified.
@article{balasingham2024material, author={Jonathan Balasingham and Viktor Zamaraev and Vitaliy Kurlin}, title = {Material Property Prediction using Graphs based on Generically Complete Isometry Invariants}, journal = {Integrating Materials and Manufacturing Innovation}, volume={13}, pages={555-568}, year = {2024}, doi={10.1007/s40192-024-00351-9} }
Back to Top of this page | Back to Research & papers | Back to Home page
Data-driven analysis of bottle packaging
- DOI : doi:10.1016/j.resconrec.2024.107538
- Abstract. The packaging industry faces mounting demand to integrate post-consumer recyclate (PCR). However, the complex structure-property relationships of PCRs often obscure their performance compared to virgin equivalents, posing challenges in selecting suitable PCRs for applications. Focused on extrusion blow moulding grade high-density polyethylene (HDPE), this study presents the most extensive characterisation of HDPE PCR to date, encompassing 23 resins (3 virgin, 20 PCR). Employing Fourier-transform infrared spectroscopy (FTIR), differential scanning calorimetry (DSC), thermogravimetric analysis (TGA), rheology, colour analysis, and mechanical testing, we established a feature-rich dataset with 56 distinctive characteristics. Utilising a data science approach based on principal component analysis, with the virgin samples as a benchmark, we identified that combining FTIR, TGA and mechanical testing provided effective identification of PCRs that closely match the properties of virgin HDPE. The pipeline created can be utilised for new PCRs to determine suitability as a replacement for virgin plastic in a desired application.
@article{smith2024, title={A data-driven analysis of HDPE post-consumer recyclate for sustainable bottle packaging}, author={Philip Smith and Andy McLauchlin and Tom Franklin and Peiyao Yan and Emily Cunliffe and Tom Hasell and Vitaliy A Kurlin and Colin Kerr and Jonathan Attwood and Michael P Shaver and Tom P McDonald}, journal={Resources, Conservation and Recycling}, volume={205}, pages={107538}, year={2024} }
Back to Top of this page | Back to Research & papers | Back to Home page
Lattice energy predictions by continuous isometry invariants
 |
|
- DOI : 10.1007/978-3-031-12285-9_11
- Abstract. Crystal Structure Prediction (CSP) aims to discover solid crystalline materials by optimizing periodic arrangements of atoms, ions or molecules. CSP takes weeks of supercomputer time because of slow energy minimizations for millions of simulated crystals. The lattice energy is a key physical property, which determines thermodynamic stability of a crystal but has no simple analytic expression. Past machine learning approaches to predict the lattice energy used slow crystal descriptors depending on manually chosen parameters. The new area of Periodic Geometry offers much faster isometry invariants that are also continuous under perturbations of atoms. Our experiments on simulated crystals confirm that a small distance between the new invariants guarantees a small difference of energies. We compare several kernel methods for invariant-based predictions of energy and achieve the mean absolute error of less than 5kJ/mole or 0.05eV/atom on a dataset of 5679 crystals.
@inproceedings{ropers2022fast, title={Fast predictions of lattice energies by continuous isometry invariants of crystal structures}, author={Ropers, Jakob and Mosca, Marco M and Anosova, Olga D and Kurlin, Vitaliy A and Cooper, Andrew I}, booktitle={International Conference on Data Analytics and Management in Data Intensive Domains}, pages={178-192}, year={2022} }
Back to Top of this page | Back to Research & papers | Back to Home page

