Project Cloud Isometry Spaces within a new area of Geometric Data Science based on papers
MATCH 2024
CVPR 2023
Maths 2021
MFCS 2020
- Cloud Isometry Spaces are moduli spaces of finite clouds of unordered points up to rigid motion or isometry.
- The related area of Periodic Geometry studies moduli spaces of periodic point sets that model all periodic crystals.
- The applied area of Computational Materials Science explores practical applications of geometric invariants and metrics.
- The even wider area of Geometric Data Science studies moduli spaces of any data objects up to practical equivalences.
- The latest developments are discussed in the MIF++ seminar and at the annual conference MACSMIN since 2020.
Complete polynomial-time invariants of unordered point clouds
 |
|
- DOI : 10.46793/match.91-1.079K
- Abstract. The most fundamental model of a molecule is a cloud of unordered atoms, even without chemical bonds that can depend on thresholds for distances and angles. The strongest equivalence between clouds of atoms is rigid motion, which is a composition of translations and rotations. The existing datasets of experimental and simulated molecules require a continuous quantification of similarity in terms of a distance metric. While clouds of m ordered points were continuously classified by Lagrange’s quadratic forms (distance matrices or Gram matrices), their extensions to m unordered points are impractical due to the exponential number of m! permutations. We propose new metrics that are continuous in general position and are computable in a polynomial time in the number m of unordered points in any Euclidean space of a fixed dimension n.
@article{kurlin2024polynomial, title={Polynomial-time algorithms for continuous metrics on atomic clouds of unordered points}, author={Vitaliy Kurlin}, journal={MATCH Communications in Mathematical and in Computer Chemistry}, year={2024}, volume={91}, issue={1}, pages={79-108} }
Back to Top of this page | Back to Research & papers | Back to Home page
Complete and continuous invariants of unordered point clouds

|
|
- Abstract. Rigid structures such as cars or any other solid objects are often represented by finite clouds of unlabeled points. The most natural equivalence on these point clouds is rigid motion or isometry maintaining all inter-point distances. Rigid patterns of point clouds can be reliably compared only by complete isometry invariants that can also be called equivariant descriptors without false negatives (isometric clouds having different descriptions) and without false positives (non-isometric clouds with the same description). Noise and motion in data motivate a search for invariants that are continuous under perturbations of points in a suitable metric. We propose the first continuous and complete invariant of unlabeled clouds in any Euclidean space. For a fixed dimension, the new metric for this invariant is computable in a polynomial time in the number of points.
@inproceedings{widdowson2023recognizing, title={Recognizing rigid patterns of unlabeled point clouds by complete and continuous isometry invariants with no false negatives and no false positives}, author={Daniel E Widdowson and Vitaliy A Kurlin}, booktitle={Computer Vision and Pattern Recognition}, year={2023}, pages={1275-1284} }
Back to Top of this page | Back to Research & papers | Back to Home page
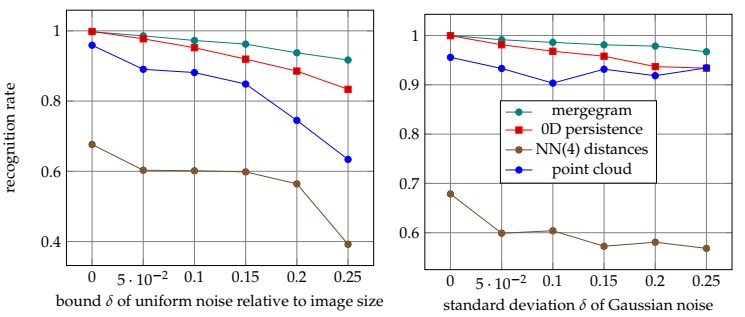
Isometry invariant shape recognition
 |
|
@article{elkin2021isometry, author = {Elkin, Y. and Kurlin, V.}, title = {Isometry invariant shape recognition of projectively perturbed point clouds by the mergegram extending 0D persistence}, journal = {Mathematics}, volume = {9}, year = {2021}, number = {17}, article-number = {2121} }- DOI : 10.3390/math9172121
- Abstract. Rigid shapes should be naturally compared up to rigid motion or isometry, which preserves all inter-point distances. The same rigid shape can be often represented by noisy point clouds of different sizes. Hence, the isometry shape recognition problem requires methods that are independent of a cloud size. This paper studies stable-under-noise isometry invariants for the recognition problem stated in the harder form when given clouds can be related by affine or projective transformations. The first contribution is the stability proof for the invariant mergegram, which completely determines a single-linkage dendrogram in general position. The second contribution is the experimental demonstration that the mergegram outperforms other invariants in recognizing isometry classes of point clouds extracted from perturbed shapes in images.
Back to Top of this page | Back to Research & papers | Back to Home page
The mergegram of a dendrogram
 |
|
@inproceedings{elkin2020mergegram, author = {Elkin, Y. and Kurlin, V.}, title = {The mergegram of a dendrogram and its stability}, booktitle = {Proceedings of MFCS (Mathematical Foundations of Computer Science)}, pages={32:1-32:13}, doi = {10.4230/LIPIcs.MFCS.2020.32}, year = {2020} }- DOI : 10.4230/LIPIcs.MFCS.2020.32
- Input : a dendrogram D of any hierarchical clustering on a point cloud.
- Output : the mergegram of the dendrogram D consisting of stable (birth,death) pairs of all intermediate clusters.
- Abstract. This paper extends the key concept of persistence within Topological Data Analysis (TDA) in a new direction. TDA quantifies topological shapes hidden in unorganized data such as clouds of unordered points. In the 0-dimensional case the distance-based persistence is determined by a single-linkage (SL) clustering of a finite set in a metric space. Equivalently, the 0D persistence captures only edge-lengths of a Minimum Spanning Tree (MST). Both SL dendrogram and MST are unstable under perturbations of points. We define the new stable-under-noise mergegram, which outperforms previous isometry invariants on a classification of point clouds by PersLay.
Back to Top of this page | Back to Research & papers | Back to Home page
