Project Geometry of Proteins within Geometric Data Science based on papers
Acta Cryst D 2025
MATCH 2025
MathVis 2017
Geometry of Proteins classifies tertiary structures of proteins under rigid motion
- The wider area of Geometric Data Science studies moduli spaces of any real data objects up to practical equivalences.
- The adjacent area of Cloud Isometry Spaces develops continuous parametrizations for finite clouds of unordered points.
- The applied area of Computational Materials Science explores practical applications of geometric invariants and metrics.
- The latest developments are discussed in the MIF++ seminar and at the annual conference MACSMIN since 2020.
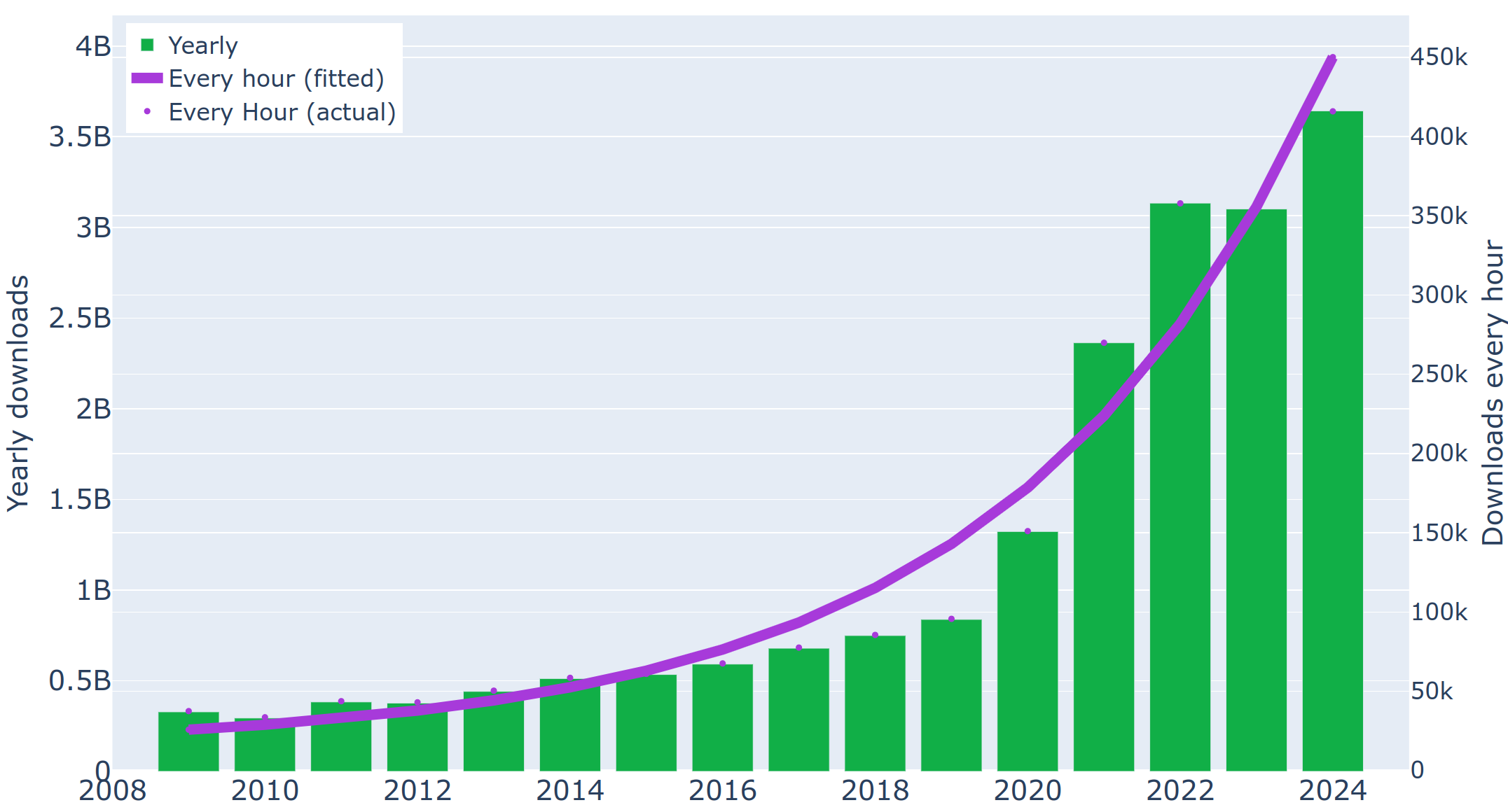
Duplicate entries in the Protein Data Bank
 |
|
- Abstract. A global analysis of protein crystal structures in the Protein Data Bank (PDB) using a newly developed computational approach reveals many pairs with (nearly) identical main-chain coordinates. Such cases are identified and analyzed, showing that duplication is possible since the PDB does not currently have tools or mechanisms that would detect potentially duplicate submissions. Some duplicated entries represent modeling efforts of ligand binding that masquerade as experimentally determined structures.We propose that duplicate entries should either be obsoleted by the PDB or, as a minimum, marked with a clear ‘CAVEAT’ record that would alert potential users to the presence of such problems. We also suggest that using a tool for verifying the uniqueness of the deposited structure, such as that presented in this work, should become part of the routine validation procedure for new depositions.
@article{wlodawer2025duplicate, title={Duplicate entries in the Protein Data Bank: how to detect and handle them}, author={A Wlodawer and Z Dauter and P Rubach and W Minor and M Jaskolski and W Jeffcott and Z Jiang and O Anosova and V Kurlin}, journal={Acta Crystallographica Section D}, volume={81}, issue={4}, pages={170-180}, year={2025} }
Back to Top of this page | Back to Research & papers | Back to Home page
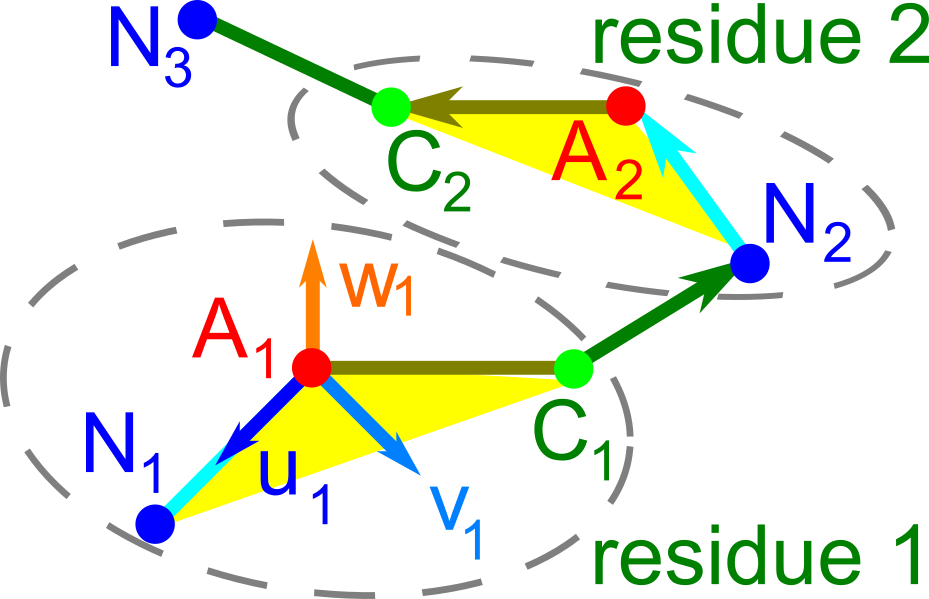
Backbone rigid invariant of protein tertiary structures
 |
|
- Abstract. Proteins are large biomolecules that regulate all living organisms and consist of one or several chains. The primary structure of a protein chain is a sequence of amino acid residues whose three main atoms (alpha-carbon, nitrogen, and carbonyl carbon) form a protein backbone. The tertiary structure is the rigid shape of a protein chain represented by atomic positions in 3-dimensional space. Because different geometric structures often have distinct functional properties, it is important to continuously quantify differences in rigid shapes of protein backbones. Unfortunately, many widely used similarities of proteins fail axioms of a distance metric and discontinuously change under tiny perturbations of atoms. This paper develops a complete invariant that identifies any protein backbone in 3-dimensional space, uniquely under rigid motion. This invariant is Lipschitz bi-continuous in the sense that it changes up to a constant multiple of a maximum perturbation of atoms, and vice versa. The new invariant has been used to detect thousands of (near-)duplicates in the Protein Data Bank, whose presence inevitably skews machine learning predictions.The resulting invariant space allows low-dimensional maps with analytically defined coordinates that reveal substantial variability in the protein universe.
@article{anosova2025complete, title={A complete and bi-continuous invariant of protein backbones under rigid motion}, author={Olga Anosova and Alexey Gorelov and William Jeffcott and Ziqiu Jiang and Vitaliy Kurlin}, journal={MATCH Comm. Math. Comp. Chemistry}, volume={94}, issue={1}, pages={97-134}, year={2025} }
Back to Top of this page | Back to Research & papers | Back to Home page
Invariants of knotted graphs given by sequences of points
 |
|
- Abstract. We design a fast algorithm for computing the fundamental group of the complement to any knotted polygonal graph in 3-space. A polygonal graph consists of straight segments and is given by sequences of vertices along edge-paths. This polygonal model is motivated by protein backbones described in the Protein Data Bank by 3D positions of atoms. The KGG algorithm simplifies a knotted graph and computes a short presentation of the Knotted Graph Group containing powerful invariants for classifying graphs up to isotopy. We use only a reduced plane diagram without building a large complex representing the complement of a graph in 3-space.
@incollection{kurlin2017computing, author = {Kurlin,V.}, title = {Computing invariants of knotted graphs given by sequences of points in 3-dimensional space}, booktitle = {Mathematics and Visualization IV (post-proceedings of TopoInVis 2015)}, publisher = {Springer}, pages = {349-363}, year = {2017} }- Input : 3D coordinates of vertices of a polygonal chain K.
- Output : a presentation of the fundamental group of R3 - K.
- Running time : O(n2) for the length n of a polygonal chain K.
- C++ code : invariants-knotted-graphs.cpp, e-mail vitaliy.kurlin@gmail.com for support.
- Demo input : file with 3D coordinates trefoil.txt.
- Input PDB files from Protein Data Bank: 1V2X, 3OIL, 3OYS, 2RH3, 3NOU, 3NOT, 3NOP, 3ZQ5.
Back to Top of this page | Back to Research & papers | Back to Home page
