Periodic Geometry within a new area of Geometric Data Science based on papers in
NeurIPS 2022
PRE 2022
MATCH 2022
ISVC 2022
DGMM 2022
SoCG 2021
DGMM 2021
- Periodic Geometry develops continuous parameterisations for moduli spaces of periodic point sets up to isometry.
- The subarea called Lattice Geometry studies moduli spaces of simpler periodic lattices in low dimensions 2 and 3.
- The related area of Computational Materials Science explores practical applications of geometric invariants and metrics.
- The wider area of Geometric Data Science studies moduli spaces of any data objects up to practical equivalences.
- The latest developments are discussed in the MIF++ seminar and at the annual conference MACSMIN since 2020.
Resolving the data ambiguity for periodic crystals

|
|
@article{widdowson2022resolving, title={Resolving the data ambiguity for periodic crystals}, author={Daniel Widdowson and Vitaliy Kurlin}, journal={Advances in Neural Information Processing Systems (Proceedings of NeurIPS 2022)}, volume={35}, year={2022} }- Abstract. The fundamental model of any solid crystalline material (crystal) at the atomic scale is a periodic point set. The strongest natural equivalence of crystals is rigid motion or isometry that preserves all inter-atomic distances. Past comparisons of periodic structures often used manual thresholds, symmetry groups and reduced cells, which are discontinuous under perturbations or thermal vibrations of atoms. This work defines the infinite sequence of continuous isometry invariants (Average Minimum Distances) to progressively capture distances between neighbours. The asymptotic behaviour of the new invariants is theoretically proved in all dimensions for a wide class of sets including non-periodic. The proposed near linear time algorithm identified all different crystals in the world's largest Cambridge Structural Database over a few hours on a modest desktop. The computational strength provides rigorous foundations to continuously parameterise the space of all real periodic crystals as a high-dimensional extension of Mendeleev's periodic table of elements.
Back to Top of this page | Back to Research & papers | Back to Home page
Densest packings of regular polygons
 |
|
@article{torda2022densest, title={Densest plane group packings of regular polygons}, author={Miloslav Torda and John Y Goulermas and Vitaliy A Kurlin and Graeme M Day}, journal={Physical Review E}, volume = {106}, issue = {5}, pages = {054603}, year={2022} }- DOI : 10.1103/PhysRevE.106.054603
- Abstract. Packings of regular convex polygons (n-gons) that are sufficiently dense have been studied extensively in the context of modeling physical and biological systems as well as discrete and computational geometry. Former results were mainly regarding densest lattice or double-lattice configurations. Here we consider all 2-dimensional crystallographic symmetry groups (plane groups) by restricting the configuration space of the general packing problem of congruent copies of a compact subset of the 2-dimensional Euclidean space to particular isomorphism classes of the discrete group of isometries. We formulate the plane group packing problem as a nonlinear constrained optimization problem. By means of the Entropic Trust Region Packing Algorithm that approximately solves this problem, we examine some known and unknown densest packings of various n-gons in all 17 plane groups and state conjectures about common symmetries of the densest plane group packings for every n-gon.
Back to Top of this page | Back to Research & papers | Back to Home page
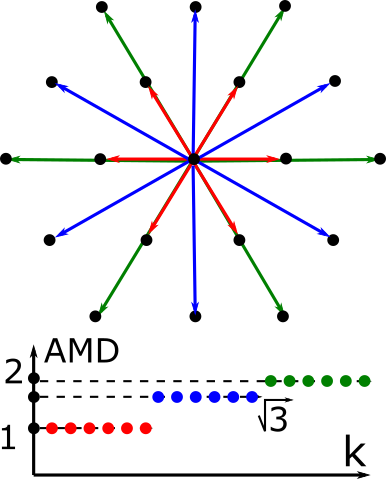
Average Minimum Distances of periodic point sets

|
|
@article{widdowson2022average, title={Average Minimum Distances of periodic point sets - fundamental invariants for mapping all periodic crystals}, author={Daniel Widdowson and Marco Mosca and Angeles Pulido and Andrew Cooper and Vitaliy Kurlin}, journal={MATCH Communications in Mathematical and in Computer Chemistry}, volume={87}, issue={3}, pages={529-559}, year={2022} }- DOI : 10.46793/match.87-3.529W
- Abstract. The fundamental model of any solid crystalline material (crystal) at the atomic scale is a periodic point set. The strongest natural equivalence of crystals is rigid motion or isometry that preserves all inter-atomic distances. Past comparisons of periodic structures often used manual thresholds, symmetry groups and reduced cells, which are discontinuous under perturbations or thermal vibrations of atoms. This work defines the infinite sequence of continuous isometry invariants (Average Minimum Distances) to progressively capture distances between neighbours. The asymptotic behaviour of the new invariants is theoretically proved in all dimensions for a wide class of sets including non-periodic. The proposed near linear time algorithm identified all different crystals in the world's largest Cambridge Structural Database over a few hours on a modest desktop. The computational strength provides rigorous foundations to continuously parameterise the space of all real periodic crystals as a high-dimensional extension of Mendeleev's periodic table of elements.
Back to Top of this page | Back to Research & papers | Back to Home page
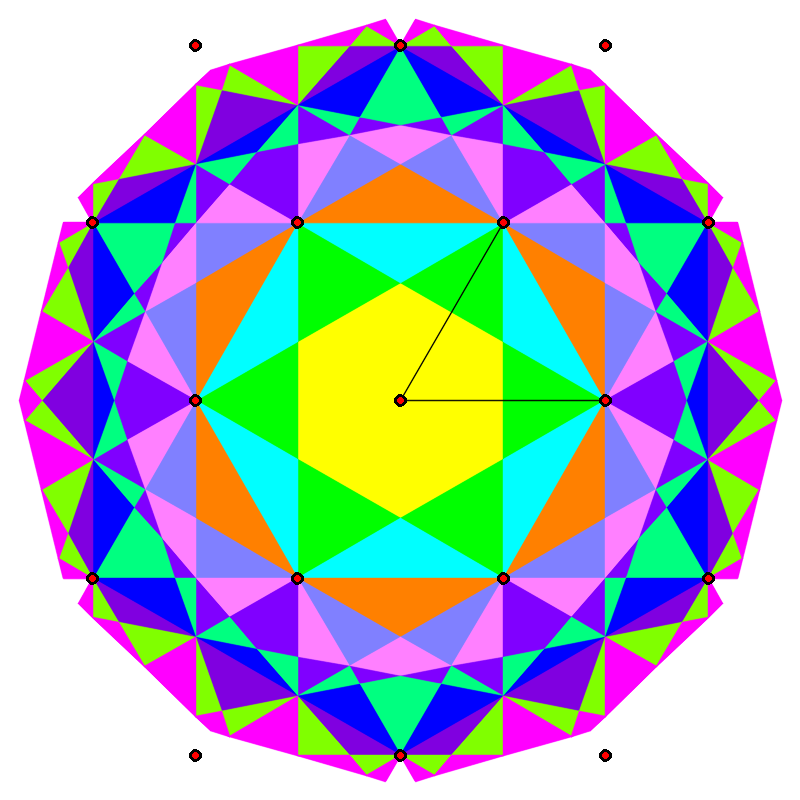
Higher degree Voronoi domains of periodic point sets
|
|
@inproceedings{smith2022practical, title={A practical algorithm for degree-k Voronoi domains of three-dimensional periodic point sets}, author={Phil Smith and Vitaliy Kurlin}, booktitle={Lecture Notes in Computer Science (Proceedings of ISVC)}, volume={13599}, year={2022} }- Abstract. Degree-k Voronoi domains of a periodic point set are concentric regions around a fixed centre consisting of all points in Euclidean space that have the centre as their k-th nearest neighbour. Periodic point sets generalise the concept of a lattice by allowing multiple points to appear within a unit cell of the lattice. Thus, periodic point sets model all solid crystalline materials (periodic crystals), and degree-k Voronoi domains of periodic point sets can be used to characterise the relative positions of atoms in a crystal from a fixed centre. The paper describes the first algorithm to compute all degree-$ Voronoi domains up to any degree k>0 for any two or three-dimensional periodic point set.
Back to Top of this page | Back to Research & papers | Back to Home page
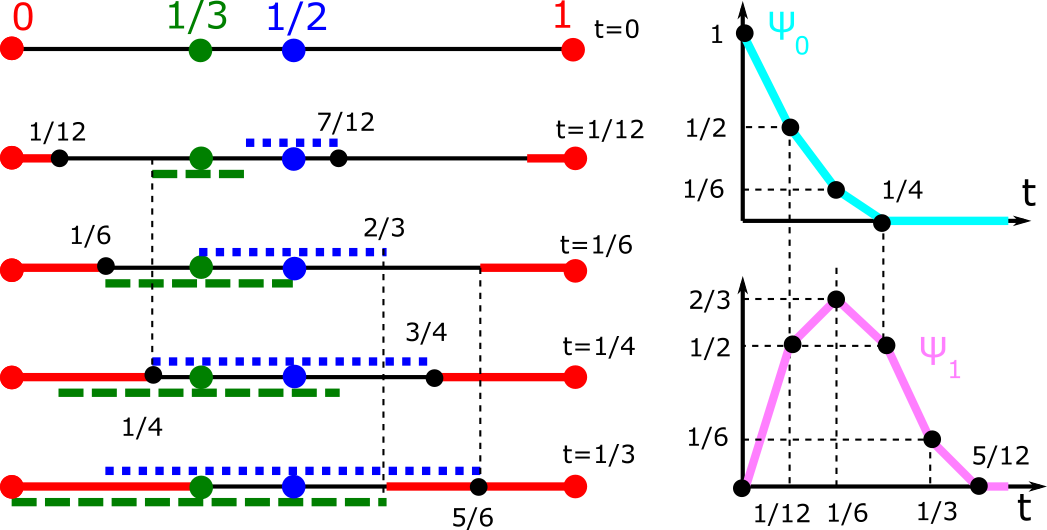
Density functions of periodic sequences
|
|
@inproceedings{anosova2022density, title={Density functions of periodic sequences}, author={Olga Anosova and Vitaliy Kurlin}, booktitle={Lecture Notes in Computer Science (Proceedings of DGMM)}, volume={13493}, pages={395-408}, year={2022} }- DOI : 10.1007/978-3-031-19897-7_31
- Abstract. This paper contributes to the emergent area of Periodic Geometry, which studies continuous spaces of solid crystalline materials (crystals) by new methods of metric geometry. Since crystal structures are determined in a rigid form, their strongest practical equivalence is rigid motion or isometry preserving inter-point distances. The most fundamental model of any crystal is a periodic set of points at all atomic centers. The previous work introduced an infinite sequence of density functions that are continuous isometry invariants of periodic point sets. These density functions turned out to be highly non-trivial even in dimension 1 for periodic sequences of points in the line. This paper fully describes the density functions of any periodic sequence and their symmetry properties. The explicit description confirms coincidences of density functions that were previously computed only through finite samples.
Back to Top of this page | Back to Research & papers | Back to Home page
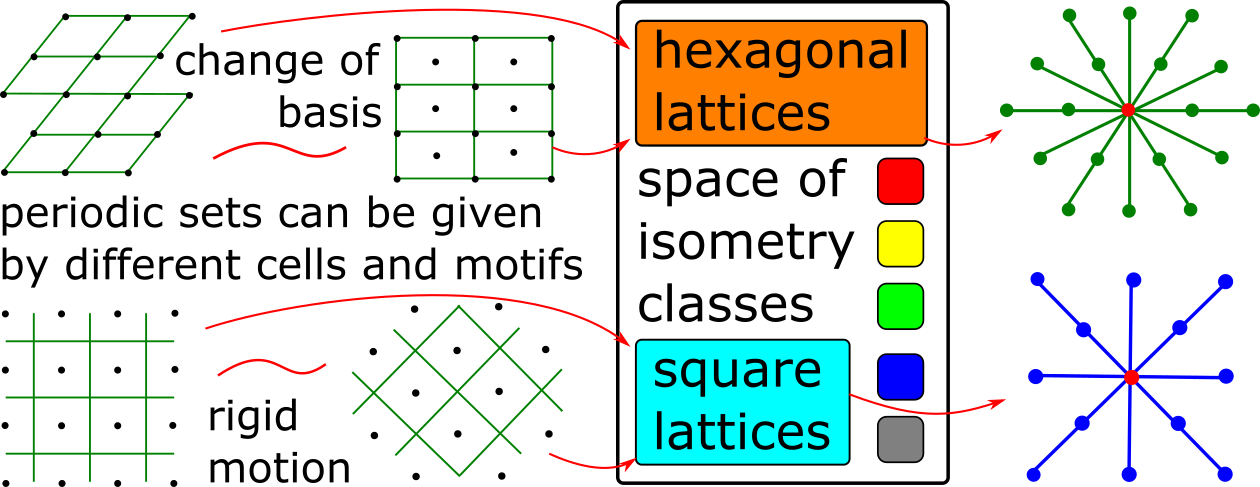
Density functions of a periodic point set

 |
|
@inproceedings{edelsbrunner2021density, title={The Density Fingerprint of a Periodic Point Set}, author={Herbert Edelsbrunner and Teresa Heiss and Vitaliy Kurlin and Philip Smith and Mathijs Wintraecken}, booktitle={Proceedings of Symposium on Computational Geometry}, pages={32:1--32:16}, year={2021} }- DOI : 10.4230/LIPIcs.SoCG.2021.32
- Abstract. Modeling a crystal as a periodic point set, we present a fingerprint consisting of density functions that facilitates the efficient search for new materials. We prove invariance under isometries, continuity, and completeness in the generic case, which are necessary features for the reliable comparison of crystals. The proof of continuity integrates methods from discrete geometry and lattice theory, while the proof of generic completeness combines techniques from geometry with analysis. The fingerprint has a fast algorithm based on Brillouin zones and related inclusion-exclusion formulae. We have implemented the algorithm and describe its application to crystal structure prediction.
Back to Top of this page | Back to Research & papers | Back to Home page
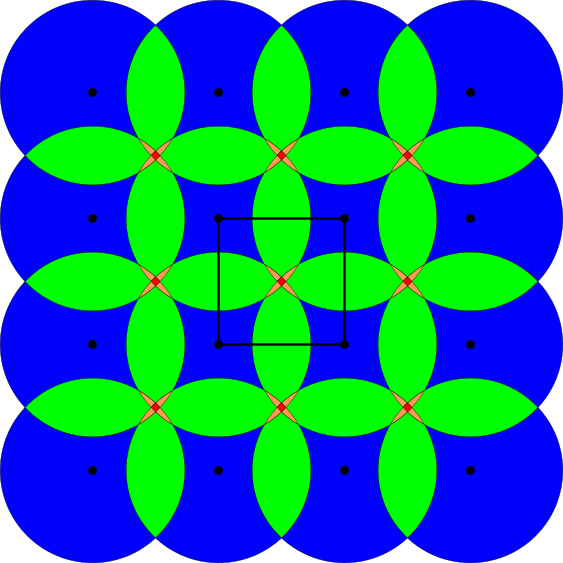
Crystal isosets are complete isometry invariants
 |
|
@inproceedings{anosova2021isometry, title={An isometry classification of periodic point sets}, author={Anosova, Olga and Kurlin, Vitaliy}, booktitle={Lecture Notes in Computer Science (Proceedings of DGMM)}, volume={12708}, pages={229-241}, year={2021} }- DOI : 10.1007/978-3-030-76657-3_16
- Abstract. We develop discrete geometry methods to resolve the data ambiguity challenge for periodic point sets to accelerate materials discovery. In any high-dimensional Euclidean space, a periodic point set is obtained from a finite set (motif) of points in a parallelepiped (unit cell) by periodic translations of the motif along basis vectors of the cell. An important equivalence of periodic sets is a rigid motion or an isometry that preserves interpoint distances. This equivalence is motivated by solid crystals whose periodic structures are determined in a rigid form. Crystals are still compared by descriptors that are either not isometry invariants or depend on manually chosen tolerances or cut-off parameters. All discrete invariants including symmetry groups can easily break down under atomic vibrations, which are always present in real crystals. We introduce a complete isometry invariant for all periodic sets of points, which can additionally carry labels such as chemical elements. The main classification theorem says that any two periodic sets are isometric if and only if their proposed complete invariants (called isosets) are equal. A potential equality between isosets can be checked by an algorithm, whose computational complexity is polynomial in the number of motif points. The key advantage of isosets is continuity under perturbations, which allows us to quantify similarities between any periodic sets.
Back to Top of this page | Back to Research & papers | Back to Home page
