New area Periodic Geometry and Topology in Geometric Data Science based on papers in
MATCH 2022
DGMM 2021
SoCG 2021
CaG 2020
CRaT 2020
We develop a new continuous theory of periodic structures such as textiles and crystals. Periodic Geometry classifies all solid crystalline materials up to rigid motion or isometry that keeps crystal structures rigid. The key novelty is continuity of isometry invariants under perturbations of atoms. Periodic Topology studies 2-periodic textiles or 3-periodic crystalline networks up to periodic isotopies, which are continuous deformations through intermediate periodic structures without a fixed unit cell. Practical applications of new methods are explored in the related area of Computational Materials Science.
See the wider area of Geometric Data Science and latest work on continuous isometry invariants and computable metrics.
In 2019 we started the regular MIF++ seminar and initiated the annual conference MACSMIN in 2020.
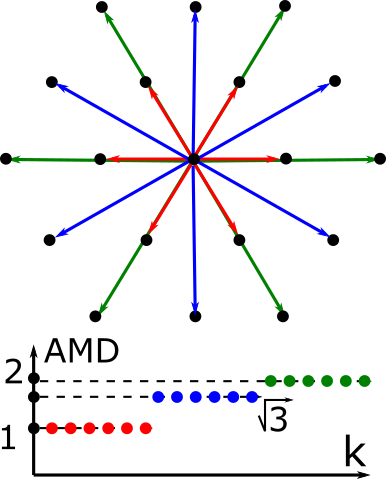
Average Minimum Distances of periodic point sets

|
|
@article{widdowson2022average, title={Average Minimum Distances of periodic point sets - fundamental invariants for mapping all periodic crystals}, author={Daniel Widdowson and Marco Mosca and Angeles Pulido and Vitaliy Kurlin and Andrew Cooper}, journal={MATCH Communications in Mathematical and in Computer Chemistry}, doi={10.46793/match.87-3.529W}, volume={87}, pages={529-559}, year={2022} }- Abstract. The fundamental model of any solid crystalline material (crystal) at the atomic scale is a periodic point set. The strongest natural equivalence of crystals is rigid motion or isometry that preserves all inter-atomic distances. Past comparisons of periodic structures often used manual thresholds, symmetry groups and reduced cells, which are discontinuous under perturbations or thermal vibrations of atoms. This work defines the infinite sequence of continuous isometry invariants (Average Minimum Distances) to progressively capture distances between neighbours. The asymptotic behaviour of the new invariants is theoretically proved in all dimensions for a wide class of sets including non-periodic. The proposed near linear time algorithm identified all different crystals in the world's largest Cambridge Structural Database over a few hours on a modest desktop. The computational strength provides rigorous foundations to continuously parameterise the space of all real periodic crystals as a high-dimensional extension of Mendeleev's periodic table of elements.
Back to Top of this page | Back to Research & papers | Back to Home page
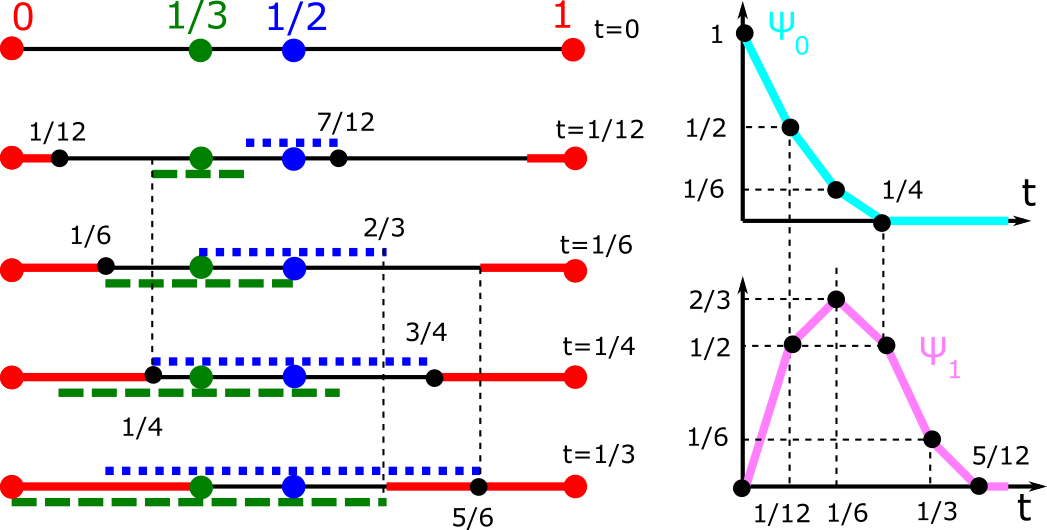
Density functions of periodic sequences
|
|
@article{anosova2022density, title={Density functions of periodic sequences}, author={Olga Anosova and Vitaliy Kurlin}, booktitle={Proceedings of Discrete Geometry and Mathematical Morphology}, year={2022} }- Abstract. This paper contributes to the emergent area of Periodic Geometry, which studies continuous spaces of solid crystalline materials (crystals) by new methods of metric geometry. Since crystal structures are determined in a rigid form, their strongest practical equivalence is rigid motion or isometry preserving inter-point distances. The most fundamental model of any crystal is a periodic set of points at all atomic centers. The previous work introduced an infinite sequence of density functions that are continuous isometry invariants of periodic point sets. These density functions turned out to be highly non-trivial even in dimension 1 for periodic sequences of points in the line. This paper fully describes the density functions of any periodic sequence and their symmetry properties. The explicit description confirms coincidences of density functions that were previously computed only through finite samples.
Back to Top of this page | Back to Research & papers | Back to Home page
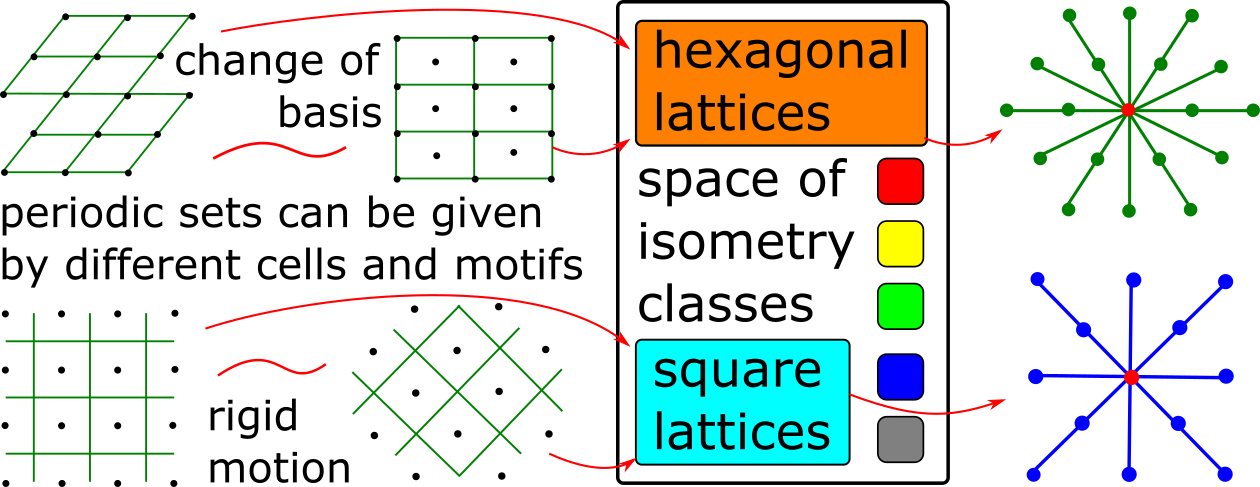
Crystal isosets are complete isometry invariants
 |
|
@inproceedings{anosova2021isometry, title={An isometry classification of periodic point sets}, author={Anosova, Olga and Kurlin, Vitaliy}, booktitle={Proceedings of Discrete Geometry and Mathematical Morphology}, doi={10.1007/978-3-030-76657-3_16}, pages={229-241}, year={2021} }- Abstract. We develop discrete geometry methods to resolve the data ambiguity challenge for periodic point sets to accelerate materials discovery. In any high-dimensional Euclidean space, a periodic point set is obtained from a finite set (motif) of points in a parallelepiped (unit cell) by periodic translations of the motif along basis vectors of the cell. An important equivalence of periodic sets is a rigid motion or an isometry that preserves interpoint distances. This equivalence is motivated by solid crystals whose periodic structures are determined in a rigid form. Crystals are still compared by descriptors that are either not isometry invariants or depend on manually chosen tolerances or cut-off parameters. All discrete invariants including symmetry groups can easily break down under atomic vibrations, which are always present in real crystals. We introduce a complete isometry invariant for all periodic sets of points, which can additionally carry labels such as chemical elements. The main classification theorem says that any two periodic sets are isometric if and only if their proposed complete invariants (called isosets) are equal. A potential equality between isosets can be checked by an algorithm, whose computational complexity is polynomial in the number of motif points. The key advantage of isosets is continuity under perturbations, which allows us to quantify similarities between any periodic sets.
Back to Top of this page | Back to Research & papers | Back to Home page
Density functions of a periodic point set

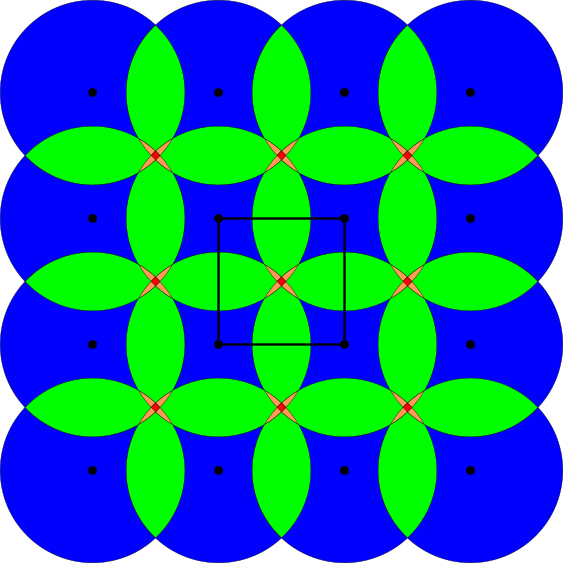
 |
|
@inproceedings{edelsbrunner2021density, title={The Density Fingerprint of a Periodic Point Set}, author={H.Edelsbrunner, T.Heiss, V.Kurlin, P.Smith, M.Wintraecken}, booktitle={Proceedings of Symposium on Computational Geometry}, pages={32:1--32:16}, doi = {10.4230/LIPIcs.SoCG.2021.32}, year={2021} }- Abstract. Modeling a crystal as a periodic point set, we present a fingerprint consisting of density functions that facilitates the efficient search for new materials. We prove invariance under isometries, continuity, and completeness in the generic case, which are necessary features for the reliable comparison of crystals. The proof of continuity integrates methods from discrete geometry and lattice theory, while the proof of generic completeness combines techniques from geometry with analysis. The fingerprint has a fast algorithm based on Brillouin zones and related inclusion-exclusion formulae. We have implemented the algorithm and describe its application to crystal structure prediction.
Back to Top of this page | Back to Research & papers | Back to Home page
Two continuous metrics on crystal lattices
 |
|
@article{mosca2020voronoi, title={Voronoi-based similarity distances between arbitrary crystal lattices}, author={Mosca, Marco and Kurlin, Vitaliy}, journal={Crystal Research and Technology}, volume={55}, number={5}, pages={190-197}, year={2020} }- Abstract. This paper develops a new continuous approach to a similarity between periodic lattices of ideal crystals. Quantifying a similarity between crystal structures is needed to substantially speed up the Crystal Structure Prediction, because the prediction of many target properties of crystal structures is computationally slow and is essentially repeated for many nearly identical simulated structures. The proposed distances between arbitrary periodic lattices of crystal structures are invariant under all rigid motions, satisfy the metric axioms and continuity under atomic perturbations. The above properties make these distances ideal tools for clustering and visualizing large datasets of crystal structures. All the conclusions are rigorously proved and justified by experiments on real and simulated crystal structures reported in the Nature 2017 paper Functional materials discovery using energy–structure–function maps.
Back to Top of this page | Back to Research & papers | Back to Home page
