This post by Phil Smith and Vitaliy Kurlin will introduce the new research area of periodic geometry. Using crystals as motivation, the periodic geometry studies periodic sets of points and their equivalence classes. We will describe the classification problem of periodic sets up to rigid motions and the work we have carried out in trying to tackle this problem.
- Crystals
- Lattices
- Unit Cells
- Periodic Sets
- Equivalency up to Rigid Motions
- Classification Problem
- Density Functions
Crystals
Solid periodic crystalline materials, or simply crystals, are everywhere, ranging from basic everyday substances like table salt to the height of luxury in diamonds. Crystals are highly geometric structures, and are good examples of real-world occurrences of periodic geometry.
This is because periodic crystals are composed of a building block (called a unit cell) that is repeated in three linearly independent directions. To study crystals from a mathematical angle, we therefore need a good grasp of this periodic geometry, so let us introduce the main objects.



Lattices
Mathematically, given $n$ ordered linearly independent vectors $v_1, v_2, …, v_n\in \mathbb{R}^n$, a lattice $\Lambda$ is defined to be the infinite set of all points that are integer linear combinations of the $v_i$, so $\Lambda = \left\{\sum\limits_{i = 1}^n c_iv_i \,|\, c_i \in \mathbb{Z}\right\}$.
As a 2D example (so $n = 2$), if we take $v_1 = (1, 0)$ and $v_2 = (0.5, \frac{\sqrt{3}}{2})$, then we get the hexagonal lattice below. Try to make out the hexagons!

The unit square lattice consists of all points with integer coordinates $(x, y)$, where $x, y \in \mathbb{Z}$. What pairs of vectors can generate this lattice? See all exercises at the end of the post.
Unit Cells
Let $\Lambda$ be a lattice generated by the vectors $v_1, …, v_n \in \mathbb{R}^n$. Restricting the coefficients of the vectors to the interval $[0, 1)$ yields a unit cell for the lattice. For the hexagonal lattice with vectors as given above, this would yield the unit cell $U_2$ in the picture below. But as the picture below shows, there are infinitely many possible unit cells for a given lattice, partly explained by the fact that there are infinitely many sets of vectors that can generate the same lattice.

In short, a unit cell is any region of the space that is spanned by some basis vectors, hence can be periodically repeated to tile the whole space.
Periodic Sets
A periodic set can be defined by a unit cell and its finite subset called a motif. The left picture below shows a unit cell for the hexagonal lattice, and a 5-point motif of the unit cell.


If we repeatedly translate the motif on the left by the given basis vectors, we get a periodic set in the right hand side picture above. Mathematically, for a motif M and a lattice $\Lambda$, a periodic set can be written as a Minkowski sum $A = M+\Lambda = \{p + v \, | \, p \in M, v \in \Lambda\}$.
To make periodic sets more practical models of real crystals, one can add chemical types or other properties of atoms or ions as labels of points. Similarly, one can represent chemical bonds with any extra information as labeled edges and get a periodic graph.
Equivalency up to Rigid Motions
Most solid crystals are rigid bodies. Hence using periodic sets as an abstract description of a crystal, it makes sense to say that two periodic sets are equivalent if they can be related to each other by a rigid motion.
A rigid motion is an operation on a space that preserves distances as well as orientation. If the space is $\mathbb{R}^3$, a rigid motion is a composition of translations and rotations around straight lines.
Are any of the three periodic sets below, with unit cells drawn, equivalent to any of the others? Feel free to submit your answer as a comment to this post.
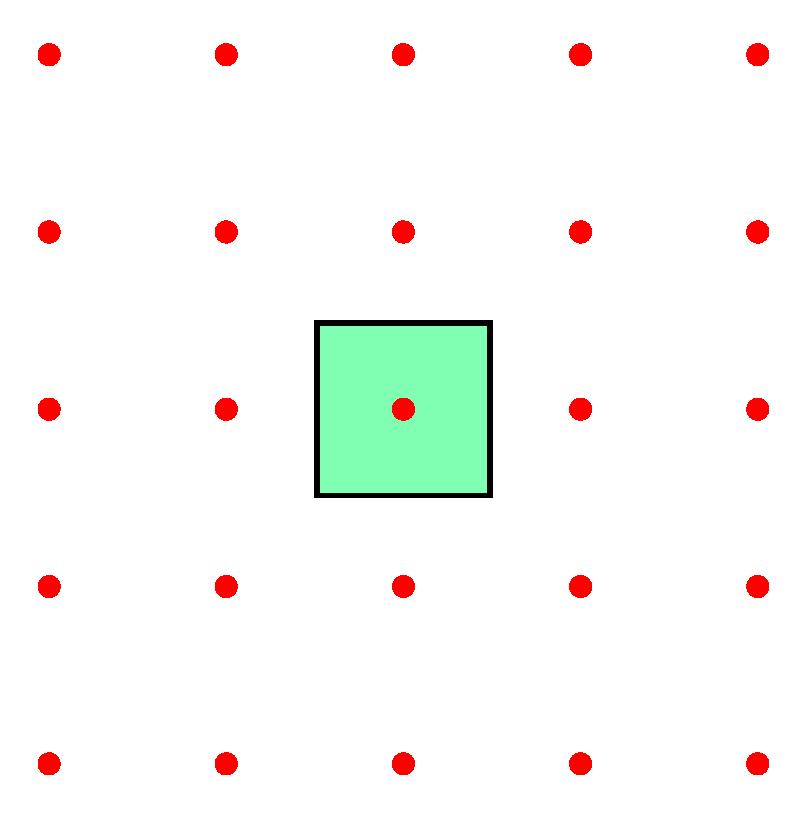

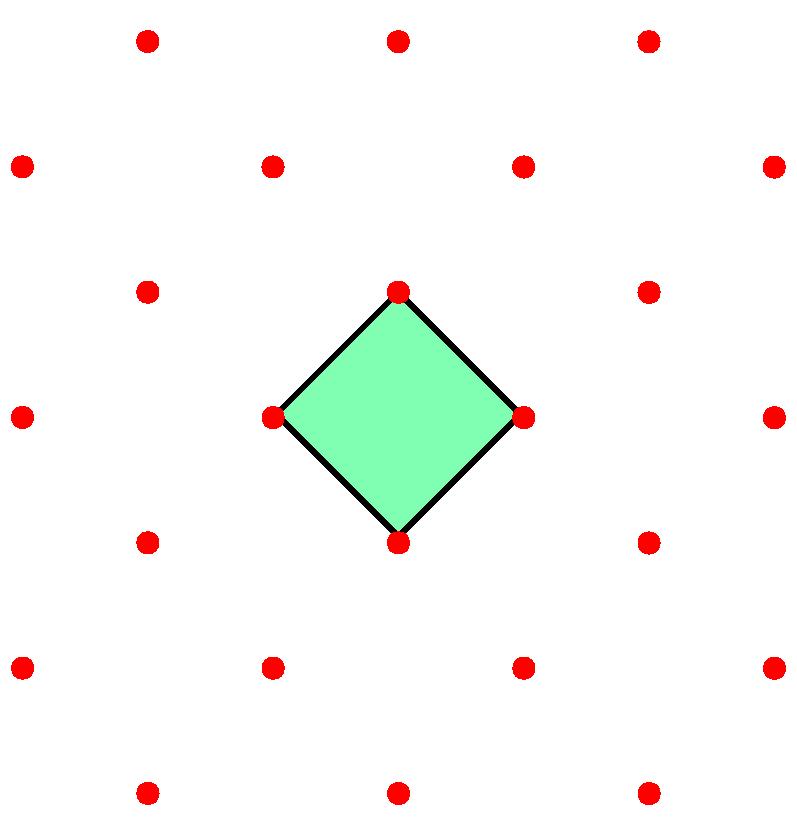
We are interested in coming up with a solution to deciding if two periodic sets are equivalent, and also by quantifying how much they differ if they are not equivalent…
Classification Problem
Treating crystals as periodic sets, we desire a fingerprint function from the complicated space of periodic sets to a simpler space, for example $\mathbb{R}^n$. There are trivial solutions to this problem, but for this fingerprint function to be helpful, we desire that it satisfies these three properties:
- Invariant under a change of unit cell and rigid motions of$\mathbb{R}^3$;
- Stable under perturbations of points in a periodic set;
- Computable in a polynomial time in the size of a motif;
- Complete, meaning that non-equivalent periodic sets are mapped to different objects.
- Invertible in the sense that any periodic set can be reconstructed from this fingerprint.
A unit cell of a crystal is not invariant under a change of basis, but its minimal volume in $\mathbb{R}^3$ is invariant. Can you give an example of a periodic set whose minimal cell discontinuously changes its volume under a small perturbation?
One well-known stable invariant is the density, which is the number of points in a motif divided by the volume of a corresponding unit cell. This single number contains too little information and can not be complete, because many non-equivalent sets have the same density.
Density Functions
Finally we introduce density functions, which we believe could be a solution to the above problem. For a periodic set $A$, we denote by $B(A;t)$ the set of all balls of radius $t$ centred at all points $a \in A$. If the periodic set $A$ has a unit cell $U$, we define the $k$-th density function $\psi_k^A(t)$ as the fractional volume of the unit cell $U$ to be covered by exactly $k$ balls of $B(A;t)$.

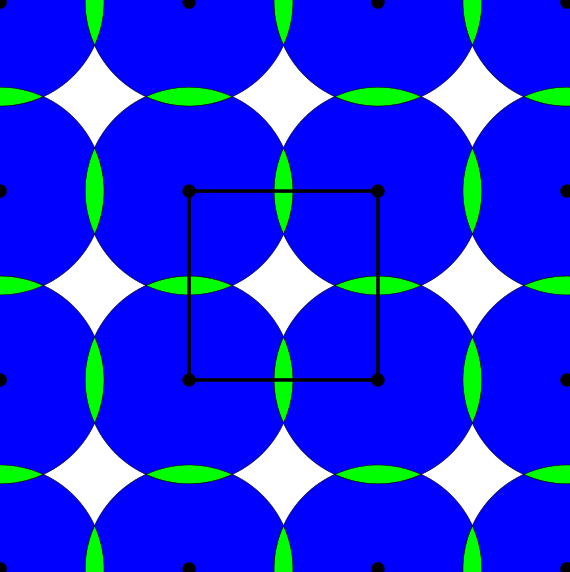
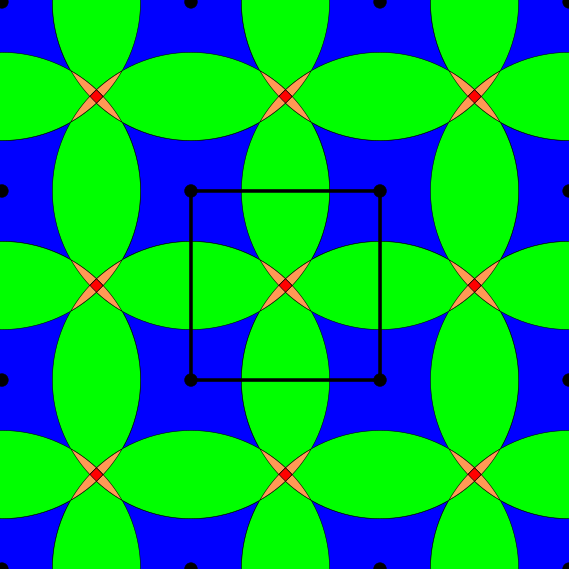


Above and below are two sets of images, the pictures above are for the square lattice and the pictures below are for the hexagonal lattice with distance 1 between closest points. In each set, the top row shows 4 images of the lattice with balls growing around each point of radii 0.25, 0.55, 0.75, 1. The bottom pictures show the eight density functions $\psi_k^{\Lambda}(t)$ for each lattice $\Lambda$.
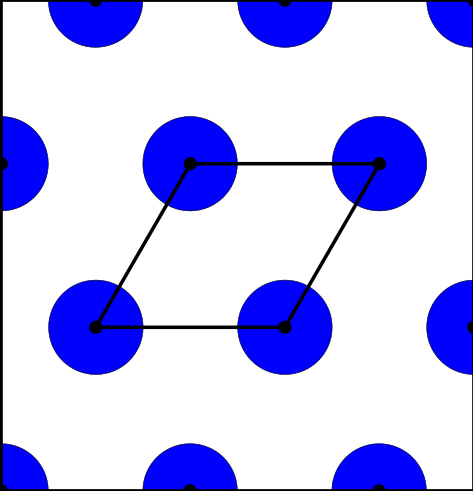
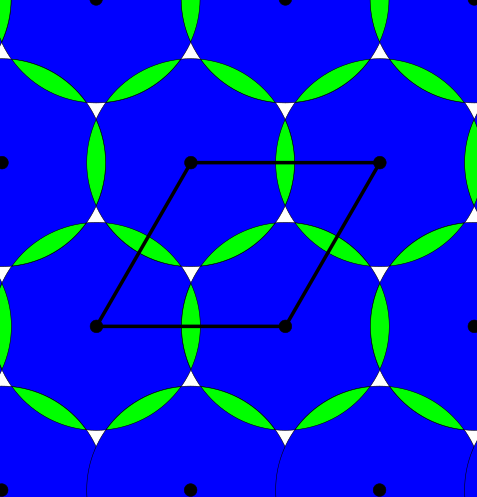
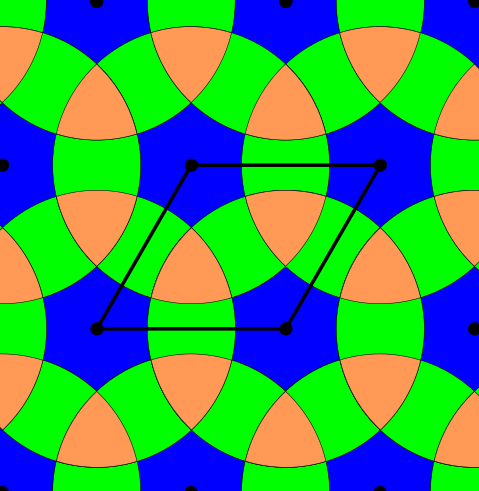

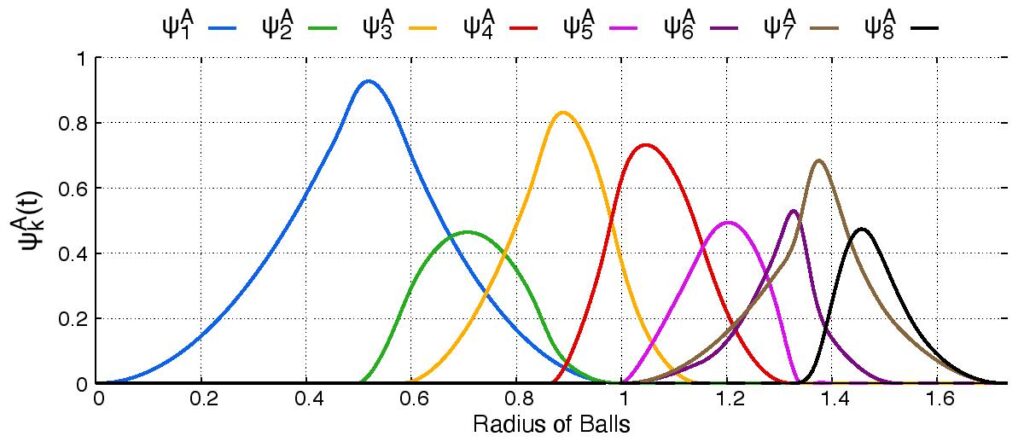
Density functions are by construction invariant under rigid motions of $\mathbb{R}^3$, and less trivially, in collaboration with Teresa Heiss, Mathijs Wintraecken and Herbert Edelsbrunner from IST Austria, we have proven the density functions are stable in this paper at SoCG 2021.
Exercises on periodic sets
- Q1. For the unit square lattice in the plane, what pairs of vectors can be a basis? Hint: there are infinitely many such pairs. Can you describe all of them?
- Q2. Which of the 3 periodic sets with red points and green unit square cells above equivalent to each other up to rigid motions and why?
- Q3. Give an example of a periodic set whose minimal cell discontinuously changes its volume under a small perturbation.
If you wish to solve the exercises, feel free to reply or email Vitaliy Kurlin.