Project Knotted structures based on papers in
CMMP 2022
NumGrid 2021
CaG 2020
MV 2017
CCIS 2016
IVAPP 2015
Invariant-based formula for the linking number
 |
|
@article{bright2022formula, title={A formula for the linking number in terms of isometry invariants of straight line segments}, author={Bright, Matthew and Anosova, Olga and Kurlin, Vitaliy}, journal={Computational Mathematics and Mathematical Physics}, volume={62}, number={8}, pages={1217–1233}, year={2022} }- Abstract. The linking number is usually defined as an isotopy invariant of two non-intersecting closed curves in 3-dimensional space. However, the original definition in 1833 by Gauss in the form of a double integral makes sense for any open disjoint curves considered up to rigid motion. Hence the linking number can be studied as an isometry invariant of rigid structures consisting of straight line segments. For the first time this paper gives a complete proof for an explicit analytic formula for the linking number of two line segments in terms of six isometry invariants, namely the distance and angle between the segments and four coordinates of their endpoints in a natural coordinate system associated with the segments. Motivated by interpenetration of crystalline networks, we discuss potential extensions to infinite periodic structures and review recent advances in isometry classifications of periodic point sets.
Back to Top of this page | Back to Research & papers | Back to Home page
Asymptotic behaviour of the linking number
 |
|
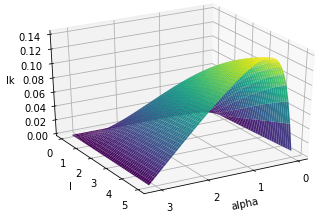@incollection{bright2021proof, title={A proof of the invariant-based formula for the linking number and its asymptotic behaviour}, author={Bright, Matt and Anosova, Olga and Kurlin, Vitaliy}, booktitle={Numerical Geometry, Grid Generation and Scientific Computing}, pages={37--60}, year={2021}, publisher={Springer} }- Abstract. In 1833 Gauss defined the linking number of two disjoint curves in 3-space. For open curves this double integral over the parameterised curves is real-valued and invariant modulo rigid motions or isometries that preserve distances between points, and has been recently used in the elucidation of molecular structures. In 1976 Banchoff geometrically interpreted the linking number between two line segments. An explicit analytic formula based on this interpretation was given in 2000 without proof in terms of 6 isometry invariants: the distance and angle between the segments and 4 coordinates specifying their relative positions. We give a detailed proof of this formula and describe its asymptotic behaviour that wasn't previously studied.
Back to Top of this page | Back to Research & papers | Back to Home page
Topological classification of textiles up to complexity five
 |
|
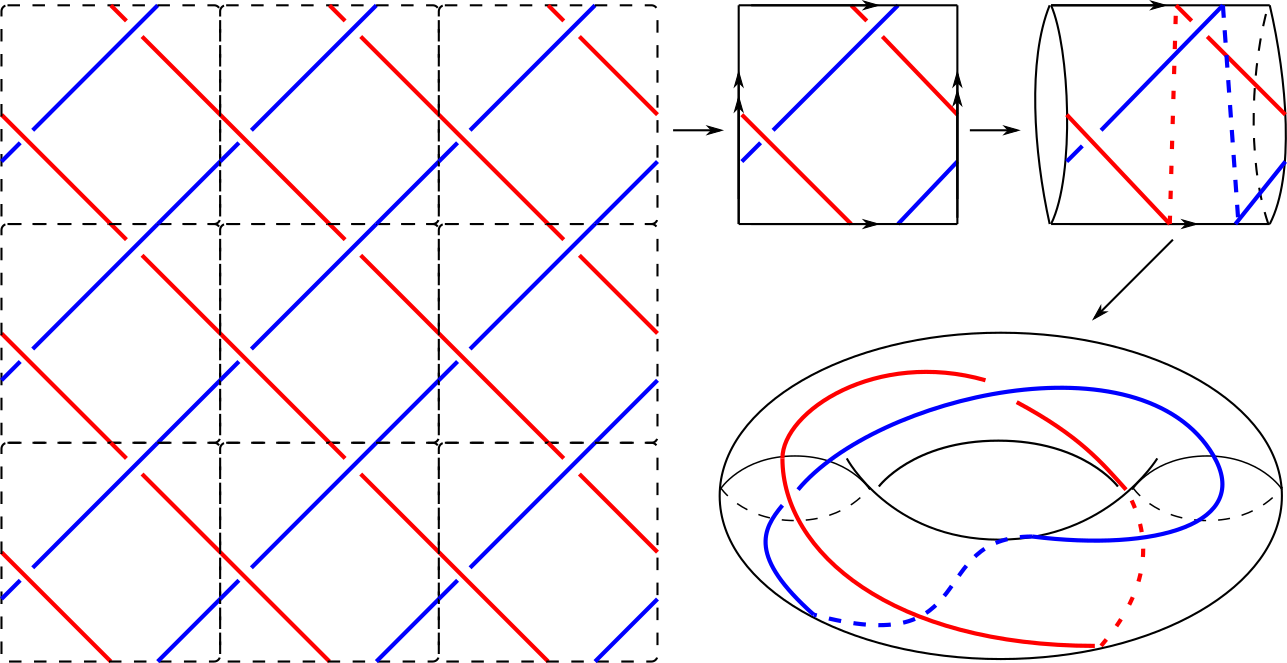@article{bright2020encoding, title={Encoding and Topological Computation on Textile Structures}, author={Bright, Matt and Kurlin, Vitaliy}, journal={Computers & Graphics}, volume = {90}, pages = {51-61}, year={2020} }- Abstract. A textile structure is a periodic arrangement of threads in the thickened plane. A topological classification of textile structures is harder than for classical knots and links that are non-periodic and restricted to a bounded region. The first important problem is to encode all textile structures in a simple combinatorial way. This paper extends the notion of the Gauss code in classical knot theory, providing a tool for topological computation on these structures. As a first application, we present a linear time algorithm for determining whether a code represents a textile in the physical sense. This algorithm, along with invariants of textile structures, allowed us for the first time to classify all oriented textile structures woven from a single component up to complexity five.
Back to Top of this page | Back to Research & papers | Back to Home page
Paper: Computing invariants of knotted graphs given by sequences of points in 3-dimensional Space.
 |
|
@incollection{Kur17MV, author = {Kurlin,V.}, title = {Computing invariants of knotted graphs given by sequences of points in 3-dimensional space}, booktitle = {Mathematics and Visualization IV (post-proceedings of TopoInVis 2015)}, publisher = {Springer}, pages = {349-363}, year = {2017} }- Abstract. We design a fast algorithm for computing the fundamental group of the complement to any knotted polygonal graph in 3-space. A polygonal graph consists of straight segments and is given by sequences of vertices along edge-paths. This polygonal model is motivated by protein backbones described in the Protein Data Bank by 3D positions of atoms. The KGG algorithm simplifies a knotted graph and computes a short presentation of the Knotted Graph Group containing powerful invariants for classifying graphs up to isotopy. We use only a reduced plane diagram without building a large complex representing the complement of a graph in 3-space.
- Input : 3D coordinates of vertices of a polygonal chain K.
- Output : a presentation of the fundamental group of R3 - K.
- Running time : O(n2) for the length n of a polygonal chain K.
- C++ code : invariants-knotted-graphs.cpp, e-mail vitaliy.kurlin@gmail.com for support.
- Demo input : file with 3D coordinates trefoil.txt. Input PDB files from Protein Data Bank: 1V2X, 3OIL, 3OYS, 2RH3, 3NOU, 3NOT, 3NOP, 3ZQ5.
Back to Top of this page | Back to Research & papers | Back to Home page
Paper: A linear time algorithm for embedding arbitrary knotted graphs into a 3-page book.
 |
|
@incollection{KS16CCIS, author = {Kurlin, V. and Smithers, C.}, title = {A linear time algorithm for embedding arbitrary knotted graphs into a 3-page book}, booktitle = {Computer Vision, Imaging and Computer Graphics Theory and Applications}, publisher = {Springer}, year = {2016}, pages = {99-122} }
Back to Top of this page | Back to Research & papers | Back to Home page
Paper: A linear time algorithm for visualizing knotted structures in 3 pages.
 |
|
@inproceedings{Kur15IVAPP, author = {Kurlin, V.}, title = {A linear time algorithm for visualizing knotted structures in 3 pages}, booktitle = {Proceedings of IVAPP 2015: Information Visualization Theory and Applications}, pages = {5-16}, publisher = {SciTePress} year = {2015} }- ISBN : 978-989-758-088-8 DOI : 10.5220/0005259900050016
- Abstract. We introduce simple codes and fast visualization tools for knotted structures in molecules and neural networks. Knots, links and more general knotted graphs are studied up to an ambient isotopy in Euclidean 3-space. A knotted graph can be represented by a plane diagram or by an abstract Gauss code. First we recognize in linear time if an abstract Gauss code represents an actual graph embedded in 3-space. Second we design a fast algorithm for drawing any knotted graph in the 3-page book, which is a union of 3 half-planes along their common boundary line. The running time of our drawing algorithm is linear in the length of a Gauss code of a given graph. Three-page embeddings provide simple linear codes of knotted graphs so that the isotopy problem for all graphs in 3-space completely reduces to a word problem in finitely presented semigroups.
- Input : a Gauss code of a plane diagram of a knotted graph in 3-space.
- Output : an embedding of the given knotted graph into the 3-page book.
- Running time : O(n) for the length n of a Gauss code of a knotted graph.
- C++ code : 3page-embeddings-graphs.cpp, e-mail vitaliy.kurlin@gmail.com for support.
Back to Top of this page | Back to Research & papers | Back to Home page