Project Topological Data Analysis based on papers in
PR 2021 |
AAM 2019 |
PRL 2016 |
CGF 2015 |
CAIP 2015 |
CVPR 2014
HoPeS = Homologically Persistent Skeleton
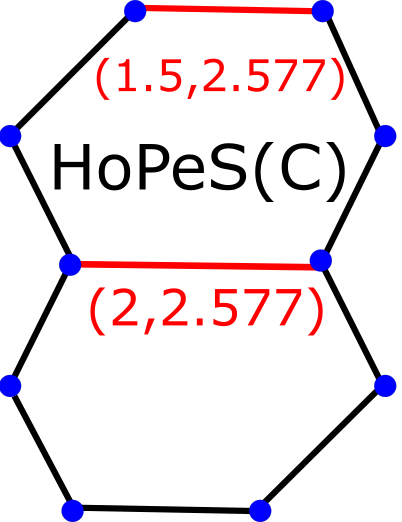
 |
|
@article{smith2021skeletonisation, title={Skeletonisation algorithms with theoretical guarantees for unorganised point clouds with high levels of noise}, author={Smith, Philip and Kurlin, Vitaliy}, journal={Pattern Recognition}, volume={115}, pages={107902}, year={2021} }- Abstract. Data Science aims to extract meaningful knowledge from unorganised data. Real datasets usually come in the form of a cloud of points with only pairwise distances. Numerous applications require to visualise an overall shape of a noisy cloud of points sampled from a non-linear object that is more complicated than a union of disjoint clusters. The skeletonisation problem in its hardest form is to find a 1-dimensional skeleton that correctly represents a shape of the cloud. This paper compares several algorithms that solve the above skeletonisation problem for any point cloud and guarantee a successful reconstruction. For example, given a highly noisy point sample of an unknown underlying graph, a reconstructed skeleton should be geometrically close and homotopy equivalent to (has the same number of independent cycles as) the underlying graph. One of these algorithm produces a Homologically Persistent Skeleton (HoPeS) for any cloud without extra parameters. This universal skeleton contains subgraphs that provably represent the 1-dimensional shape of the cloud at any scale. Other subgraphs of HoPeS reconstruct an unknown graph from its noisy point sample with a correct homotopy type and within a small offset of the sample. The extensive experiments on synthetic and real data reveal for the first time the maximum level of noise that allows successful graph reconstructions.
Back to Top of this page | Back to Research & papers | Back to Home page
Higher-dimensional skeleton HoPeS
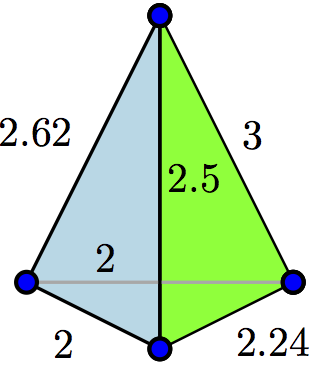 |
|
@article{kalisnik2019higher, author = {Kalisnik, S. and Kurlin,V. and Lesnik,D.}, title = {A higher-dimensional Homologically Persistent Skeleton}, journal = {Advances in Applied Mathematics}, volume = {102}, pages = {113-142}, year = {2019} }- DOI : 10.1016/j.aam.2018.07.004 ISSN : 0196-8858
- Input : a finite cloud C of n points (or a filtration of complexes on C) in any metric space.
- Output : a k-dimensional skeleton HoPeS(C) with all persistent k-dimensional cycles hidden in C.
- Abstract. Real data is often given as a point cloud, i.e. a finite set of points with pairwise distances between them. An important problem is to detect the topological shape of data — for example, to approximate a point cloud by a low-dimensional non-linear subspace such as an em- bedded graph or a simplicial complex. Classical clustering methods and principal component analysis work well when given data points split into well-separated clusters or lie near linear subspaces of a Euclidean space.
- Methods from Topological Data Analysis in general metric spaces detect more complicated patterns such as holes and voids that persist for a large interval in a 1-parameter family of shapes associated to a cloud. These features can be visualized in the form of a 1-dimensional homologically persistent skeleton, which optimally extends a minimum spanning tree of a point cloud to a graph with cycles. We generalize this skeleton to higher dimensions and prove its optimality among all complexes that preserve topological features of data at any scale.
Back to Top of this page | Back to Research & papers | Back to Home page
Persistence-based segmentation of noisy 2D clouds


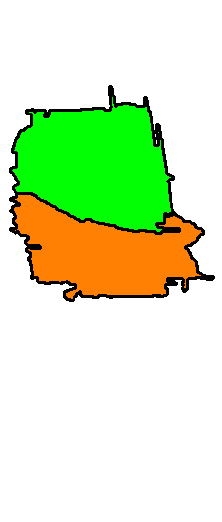
|
|
@article{kurlin2016fast, author = {Kurlin, V.}, title = {A fast persistence-based segmentation of noisy 2D clouds with provable guarantees}, journal = {Pattern Recognition Letters}, year = {2016}, volume = {83}, pages = {3-12} }- DOI : 10.1016/j.patrec.2015.11.025
- Input : a sparse noisy cloud of boundary points near unknown contours.
- Output : a segmentation into most persistent regions bounded by contours.
- Run time : O(n log n) for any n points with real coordinates in the plane.
- Abstract. We design a new fast algorithm to automatically segment a 2D cloud of points into regions. The only input is a dotted image without any extra parameters, say a scanned black-and-white map with almost closed curves or any image with detected edge points. The output is a hierarchy of segmentations into regions whose boundary contours have a long enough life span (persistence) in a sequence of nested neighborhoods of the input points. We give conditions on a noisy sample of a graph, when the boundaries of resulting regions are geometrically close to all original cycles in the unknown graph.
Back to Top of this page | Back to Research & papers | Back to Home page
HoPeS : a Homologically Persistent Skeleton
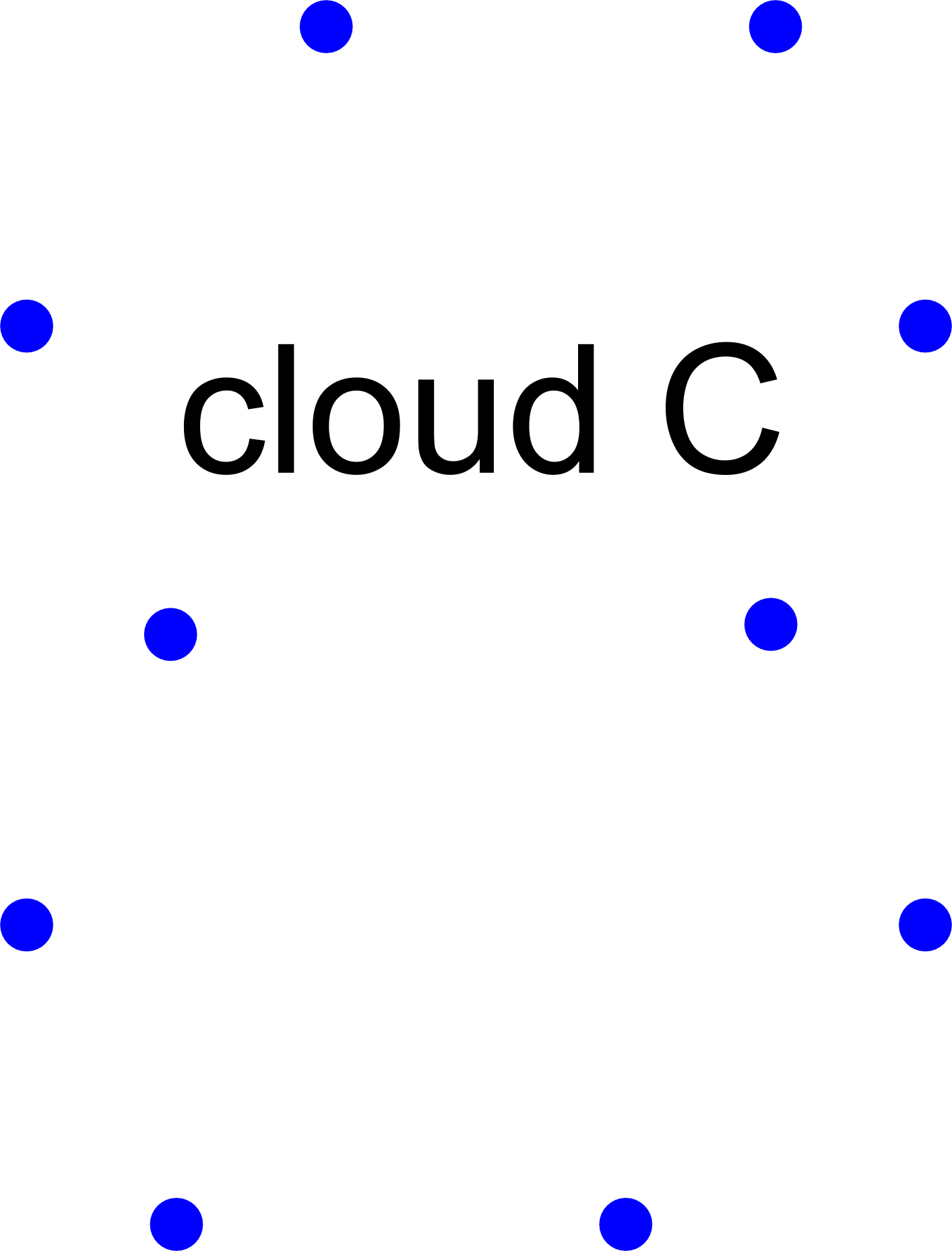
 |
|
@article{kurlin2015one, author = {Kurlin,V.}, title = {A one-dimensional Homologically Persistent Skeleton of an unstructured point cloud in any metric space}, journal = {Computer Graphics Forum}, volume = {34}, number = {5}, pages = {253-262}, year = {2015} }- DOI : 10.1111/cgf.12713 Online ISSN : 1467-8659
- Input : a finite cloud C of n points (or a filtration of complexes on C) in any metric space.
- Output : the skeleton HoPeS(C) with all persistent cycles that were hidden in the cloud C.
- Abstract. Real data are often given as a noisy unstructured point cloud, which is hard to visualize. The important problem is to represent topological structures hidden in a cloud by using skeletons with cycles. All past skeletonization methods require extra parameters such as a scale or a noise bound.
- We define a homologically persistent skeleton, which depends only on a cloud of points and contains optimal subgraphs representing 1-dimensional cycles in the cloud across all scales. The full skeleton is a universal structure encoding topological persistence of cycles directly on the cloud.
- Hence a 1-dimensional shape of a cloud can be now easily predicted by visualizing our skeleton instead of guessing a scale for the original unstructured cloud. We derive more subgraphs to reconstruct provably close approximations to an unknown graph given only by a noisy sample in any metric space. For a cloud of n points in the plane, the full skeleton and all its important subgraphs can be computed in time O(n log n).
- C++ code : persistent-skeletons.cpp (a beta-version, please e-mail vitaliy.kurlin(at)gmail.com for support).
Back to Top of this page | Back to Research & papers | Back to Home page
Persistent skeletonisation of images

 |
|
@inproceedings{kurlin2015homologically, author = {Kurlin,V.}, title = {A Homologically Persistent Skeleton is a fast and robust descriptor of interest points in 2D images}, booktitle = {Lecture Notes in Computer Science (Proceedings of CAIP 2015)}, volume = {9256}, pages = {606-617}, year = {2015} }- DOI : 10.1007/978-3-319-23192-1_51 Online ISBN : 978-3-319-23192-1
- Input : a finite cloud C of n points in the plane, say Canny edge points of a 2D image.
- Output : the skeleton HoPeS(C) whose cycles correspond to all dots in 1D persistence of C.
- Running time : O(n log n) for a cloud C of n points with any real coordinates in the plane.
- Abstract. 2D images often contain irregular salient features and interest points with non-integer coordinates. Our skeletonization problem for such a noisy sparse cloud is to summarize the topology of a given 2D cloud across all scales in the form of a graph, which can be used for combining local features into a more powerful object-wide descriptor.
- We extend a classical Minimum Spanning Tree of a cloud to a Homologically Persistent Skeleton, which
- (1) is scale-and-rotation invariant and depends only on the cloud C without any extra input parameters;
- (2) contains reduced skeleton (at every scale), shortest among all graphs that have the homology of the thickened cloud;
- (3) contains the derived skeleton giving a close approximation to a good unknown planar graph given by a noisy sample;
- (4) is geometrically stable for a noisy sample C around planar graphs (remains in a small neighborhood after perturbing C);
- (5) is computable in time O(n log n) for any n points in the plane (based on α-complexes filtering a Delaunay triangulation).
- C++ code : persistent-skeletons.cpp (a beta-version, please e-mail vitaliy.kurlin(at)gmail.com for support).
Back to Top of this page | Back to Research & papers | Back to Home page
Topologically persistent holes in noisy clouds
 |
|
@inproceedings{kurlin2014fast, author = {Kurlin, V.}, title = {A fast and robust algorithm to count topologically persistent holes in noisy clouds}, booktitle = {Proceedings of CVPR 2014: Computer Vision and Pattern Recognition}, publisher = {IEEE}, year = {2014}, pages = {1458-1463} }- DOI : 10.1109/CVPR.2014.189 Publisher : IEEE
- Input : a cloud of any points in the plane without extra parameters.
- Output : numbers of most persistent holes with associated probabilities.
- Run time : O(n log n) for any n points with real coordinates in the plane.
- Abstract. Preprocessing a 2D image often produces a noisy cloud of interest points. We study the problem of counting holes in unstructured clouds in the plane. The holes in a given cloud are quantified by the topological persistence of their boundary contours when the cloud is analyzed at all possible scales. We design the algorithm to count holes that are most persistent in the filtration of offsets (neighborhoods) around given points. The input is a cloud of n points in the plane without any user-defined parameters. The algorithm has the running time O(n log n) and space O(n). The output is the array (number of holes, relative persistence in the filtration). We prove theoretical guarantees when the algorithm finds the correct number of holes (components in the complement) of an unknown shape approximated by a cloud.
- C++ code : cloud-analysis.cpp (a beta-version, please e-mail vitaliy.kurlin(at)gmail.com for support).
Back to Top of this page | Back to Research & papers | Back to Home page
