Project Automatic cloud analysis based on papers in
AAM 2019 |
PRL 2016 |
CVPR 2014 |
CTIC 2014
Paper : Development of a Reconstruction Method for Major Vortex Structure around Tandem Flapping Wing Object via Vortex Trajectory Method.
 |
|
@inproceedings{ban2019development, title={Development of a Reconstruction Method for Major Vortex Structure around Tandem Flapping Wing Object via Vortex Trajectory Method}, author={Ban, Naohiko and Yamazaki, Wataru and Kurlin, Vitaliy}, booktitle={AIAA Scitech 2019 Forum}, pages={2224-2260}, year={2019} }- DOI : 10.1016/j.patrec.2015.11.025
- Abstract. Flapping wing micro air vehicle (MAV) is expected to apply in unmanned operations under risky / ultimate conditions. The MAV has to fly in low Reynolds number conditions. Previous researches indicated that flights by flapping motions as insects had higher performance at low Reynolds numbers. In nature, some insects have four flapping wings and achieve excellent flight performance such as hovering and steep turn. This is considered to be the effect of aerodynamic interference between fore and aft wings. The fluid mechanics of the flapping wing are, however, more difficult than traditional fixed wing due to its complex unsteady fluid physics at low Reynolds numbers. Therefore, there are various flight mechanisms within the flapping wing flight and these have not yet been fully clarified. Particle Image Velocimetry (PIV) is an efficient flow measurement technique which can measure such complex flowfield at one time. The visualization of the vorticity distribution is important for understanding the flowfield of the flapping wing object. On the other hand, however, the vorticity distribution obtained through image processing such as PIV analysis is difficult to understand the detailed vortex flowfield due to the data error or noisiness in the flowfield. In this research, therefore, we developed a reconstruction method of vorticity distribution as postprocessing method of PIV measurement for the purpose to assist the physical understanding of the noisy vorticity distribution. The developed method could clearly reconstruct small vortex structures in the backward of the flapping wing object which was difficult to discriminate by conventional vorticity visualizations.
Back to Top of this page | Back to Research & papers | Back to Home page
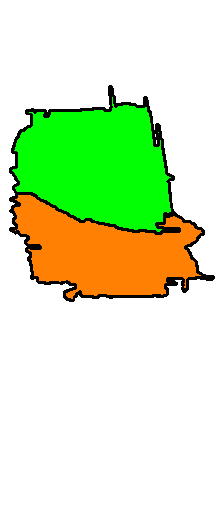
Paper: A fast persistence-based segmentation of noisy 2D clouds with provable guarantees.


|
|
@article{kurlin2016fast, author = {Kurlin, V.}, title = {A fast persistence-based segmentation of noisy 2D clouds with provable guarantees}, journal = {Pattern Recognition Letters}, year = {2016}, volume = {83}, pages = {3-12} }- DOI : 10.1016/j.patrec.2015.11.025
- Input : a sparse noisy cloud of boundary points near unknown contours.
- Output : a segmentation into most persistent regions bounded by contours.
- Run time : O(n log n) for any n points with real coordinates in the plane.
- Abstract. We design a new fast algorithm to automatically segment a 2D cloud of points into regions. The only input is a dotted image without any extra parameters, say a scanned black-and-white map with almost closed curves or any image with detected edge points. The output is a hierarchy of segmentations into regions whose boundary contours have a long enough life span (persistence) in a sequence of nested neighborhoods of the input points. We give conditions on a noisy sample of a graph, when the boundaries of resulting regions are geometrically close to all original cycles in the unknown graph.
Back to Top of this page | Back to Research & papers | Back to Home page
Paper: A fast and robust algorithm to count topologically persistent holes in noisy clouds.
 |
|
@inproceedings{kurlin2014fast, author = {Kurlin, V.}, title = {A fast and robust algorithm to count topologically persistent holes in noisy clouds}, booktitle = {Proceedings of CVPR 2014: Computer Vision and Pattern Recognition}, publisher = {IEEE}, year = {2014}, pages = {1458-1463} }- DOI : 10.1109/CVPR.2014.189 Publisher : IEEE
- Input : a cloud of any points in the plane without extra parameters.
- Output : numbers of most persistent holes with associated probabilities.
- Run time : O(n log n) for any n points with real coordinates in the plane.
- Abstract. Preprocessing a 2D image often produces a noisy cloud of interest points. We study the problem of counting holes in unstructured clouds in the plane. The holes in a given cloud are quantified by the topological persistence of their boundary contours when the cloud is analyzed at all possible scales. We design the algorithm to count holes that are most persistent in the filtration of offsets (neighborhoods) around given points. The input is a cloud of n points in the plane without any user-defined parameters. The algorithm has the running time O(n log n) and space O(n). The output is the array (number of holes, relative persistence in the filtration). We prove theoretical guarantees when the algorithm finds the correct number of holes (components in the complement) of an unknown shape approximated by a cloud.
- C++ code : cloud-analysis.cpp (a beta-version, please e-mail vitaliy.kurlin(at)gmail.com for support).
Back to Top of this page | Back to Research & papers | Back to Home page
Paper: Auto-completion of contours in sketches, maps and sparse 2D images based on topological persistence.
  |
@inproceedings{kurlin2014auto, author = {Kurlin, V.}, title = {Auto-completion of contours in sketches, maps and sparse 2D Images based on topological persistence}, booktitle = {Proceedings of SYNASC 2014 workshop CTIC: Computational Topology in Image Context}, publisher = {IEEE}, year = {2014}, pages = {594-601} }- DOI : 10.1109/SYNASC.2014.85 Print ISBN : 978-1-4799-8447-3
- Input : a cloud of any points in the plane without extra parameters.
- Output : regions that are enclosed by most persistent closed contours.
- Run time : O(n log n) for any n points with real coordinates in the plane.
- Abstract. We design a new fast algorithm to automatically complete closed contours in a finite point cloud on the plane. The only input can be a scanned map with almost closed curves, a hand-drawn artistic sketch or any sparse dotted image in 2D without any extra parameters. The output is a hierarchy of closed contours that have a long enough life span (persistence) in a sequence of nested neighbourhoods of the input points. We prove theoretical guarantees when, for a given noisy sample of a graph in the plane, the output contours geometrically approximate the original contours in the unknown graph.
- C++ code : cloud-analysis.cpp (a beta-version, please e-mail vitaliy.kurlin(at)gmail.com for support).
Back to Top of this page | Back to Research & papers | Back to Home page
